题目内容
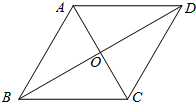 如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:
如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:(1)两条对角线的长度;
(2)菱形的面积.
考点:菱形的性质
专题:
分析:(1)由在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm,可求得△ABO是含30°角的直角三角形,AB=2cm,继而求得AC与BD的长;
(2)由菱形的面积等于其对角线积的一半,即可求得答案.
(2)由菱形的面积等于其对角线积的一半,即可求得答案.
解答:解:(1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC=
×180°=60°,
∴∠ABO=
∠ABC=30°,
∵菱形ABCD的周长是8cm.
∴AB=2cm,
∴OA=
AB=1cm,
∴OB=
=
,
∴AC=2OA=2cm,BD=2OB=2
cm;
(2)S菱形ABCD=
AC•BD=
×2×2
=2
(cm2).
∴AB=BC,AC⊥BD,AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC=
| 1 |
| 3 |
∴∠ABO=
| 1 |
| 2 |
∵菱形ABCD的周长是8cm.
∴AB=2cm,
∴OA=
| 1 |
| 2 |
∴OB=
| AB2-OA2 |
| 3 |
∴AC=2OA=2cm,BD=2OB=2
| 3 |
(2)S菱形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题考查了菱形的性质以及含30°角的直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
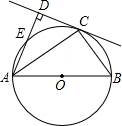 如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D. 如图,把一张长方形ABCD的纸片沿EF折叠后,ED与BC的交点为G,点D、C分别落在D′、C′的位置上,若∠EFG=55°,求∠AEG和∠EGB的度数.
如图,把一张长方形ABCD的纸片沿EF折叠后,ED与BC的交点为G,点D、C分别落在D′、C′的位置上,若∠EFG=55°,求∠AEG和∠EGB的度数.