题目内容
20.解方程(1)x2+x=2
(2)2x2-5x+2=0.
分析 (1)先把方程化为一般式,然后利用因式分解法解方程;
(2)利用因式分解法解方程.
解答 解:(1)x2+x-2=0,
(x+2)(x-1)=0,
x+2=0或x-1=0,
所以x1=-2,x2=1;
(2)(2x-1)(x-2)=0,
2x-1=0或x-2=0,
所以x1=$\frac{1}{2}$,x2=2.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
15.将y=x2向左平移3个单位长度,得( )
| A. | y=x2-3 | B. | y=x2+3 | C. | y=(x-3)2 | D. | y=(x+3)2 |
10.已知$\frac{a}{2}$=$\frac{b}{5}$,则$\frac{b-a}{a}$的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
 把如图形状的硬纸板折成一个四棱锥,那么与E点重合在一起的是A和C.
把如图形状的硬纸板折成一个四棱锥,那么与E点重合在一起的是A和C.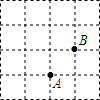 如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有( )
如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有( )
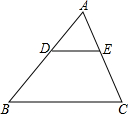 如图,在△ABC中,DE∥BC,AD=2cm,BD=3cm.
如图,在△ABC中,DE∥BC,AD=2cm,BD=3cm.