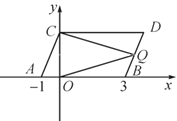
题目内容
【题目】如图,AB为⊙O的直径,AC=2,BC=4,CD=BD=DE,则CE=( )
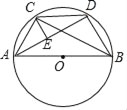
A. 3﹣![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
先根据勾股定理计算直径AB=![]() =2
=2![]() ,作垂线DP和DQ,根据角平分线的性质得:DP=DQ,由全等可得AP=AQ,设未知数列等式,可得PC和BQ的长,再根据等腰三角形的性质得:∠DEC=∠DCE,根据外角性质得:∠ACE=∠ECB,则∠ACE=∠ECB=45°,作辅助线后可得:△EFC是等腰直角三角形,设EF=FC=a,则CE=
,作垂线DP和DQ,根据角平分线的性质得:DP=DQ,由全等可得AP=AQ,设未知数列等式,可得PC和BQ的长,再根据等腰三角形的性质得:∠DEC=∠DCE,根据外角性质得:∠ACE=∠ECB,则∠ACE=∠ECB=45°,作辅助线后可得:△EFC是等腰直角三角形,设EF=FC=a,则CE=![]() a,AF=2-a,根据△AFE∽△APD,列比例式可得a的值,求CE的长.
a,AF=2-a,根据△AFE∽△APD,列比例式可得a的值,求CE的长.
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC=2,BC=4,
∴AB=![]() =2
=2![]() ,
,
∵CD=BD,
∴![]() ,
,
∴∠CAD=∠BAD,
过D作DP⊥AC于P,DQ⊥AB于Q,连接OD,
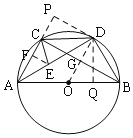
∴PD=DQ,
∴Rt△DPC≌Rt△DQB(HL),
∴CP=BQ,
易得△APD≌△AQD,
∴AP=AQ,
设PC=x,则AP=2+x,AQ=AB-BQ=2![]() -x,
-x,
∴2+x=2![]() -x,
-x,
x=![]() -1,
-1,
∴BQ=CP=![]() -1,OQ=1,
-1,OQ=1,
Rt△ODQ中,DQ=PD=![]() =2,
=2,
∵DE=DC,
∴∠DEC=∠DCE,
∵∠DEC=∠CAD+∠ACE,∠DCE=∠ECB+∠ACE,
∴∠CAD+∠ACE=∠ECB+∠DCB,
∵![]() ,
,
∴∠CAD=∠DCB,
∴∠ACE=∠ECB,
∵∠ACB=90°,
∴∠ACE=∠ECB=45°,
过E作EF⊥AP于F,
∴△EFC是等腰直角三角形,
设EF=FC=a,则CE=![]() a,AF=2-a,
a,AF=2-a,
∵EF∥PD,
∴△AFE∽△APD,
∴![]() ,
,
∴![]() ,
,
∴a=3-![]() ,
,
∴CE=![]() a=
a=![]() (3-
(3-![]() )=3
)=3![]() -
-![]() .
.
故选D.

 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】数学老师在一次“探究性学习”课中,设计了如下数表:
| 2 | 3 | 4 | 5 | … |
| 3 | 8 | 15 | 24 | … |
| 4 | 6 | 8 | 10 | … |
| 5 | 10 | 17 | 26 | … |
由表可知,当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
………
(1)当![]() 时,
时,![]() ________,
________,![]() _________,
_________,![]() ________.
________.
(2)请你分别观察![]() ,
,![]() ,
,![]() 与
与![]() 之间的关系,并分别用含有
之间的关系,并分别用含有![]() 的代数式表示
的代数式表示 ![]() ,
,![]() ,
,![]() .
.
![]() ________,
________,![]() _________,
_________,![]() ________.
________.
(3)猜想以![]() ,
,![]() ,
,![]() 为边的三角形是否为直角三角形,并说明理由.
为边的三角形是否为直角三角形,并说明理由.