题目内容
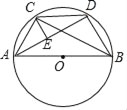
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,将弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长线交于点P,连接AD,在PB的另一侧作∠MPB=∠ADC.
(1)判断PM与⊙O的位置关系,并说明理由;
(2)若PC=![]() ,求四边形OCDB的面积.
,求四边形OCDB的面积.

【答案】(1)PM与⊙O相切,理由见解析;(2)![]() .
.
【解析】
(1)连接DO并延长交PM于E,如图,利用折叠的性质得OC=DC,BO=BD,则可判断四边形OBDC为菱形,所以OD⊥BC,△OCD和△OBD都是等边三角形,从而计算出∠COP=∠EOP=60°,接着证明PM∥BC得到OE⊥PM,所以OE=![]() OP,根据切线的性质得到OC⊥PC,则OC=
OP,根据切线的性质得到OC⊥PC,则OC=![]() OP,从而可判定PM是⊙O的切线;
OP,从而可判定PM是⊙O的切线;
(2)先在Rt△OPC中计算出OC=1,然后根据等边三角形的面积公式计算四边形OCDB的面积.
(1)PM与⊙O相切.
理由如下:连接DO并延长交PM于E,如图,
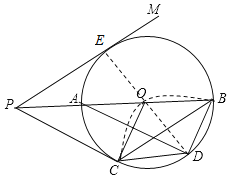
∵弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,
∴OC=DC,BO=BD,
∴OC=DC=BO=BD,
∴四边形OBDC为菱形,
∴OD⊥BC,
∴△OCD和△OBD都是等边三角形,
∴∠COD=∠BOD=60°,
∴∠COP=∠EOP=60°,
∵∠MPB=∠ADC,
而∠ADC=∠ABC,
∴∠ABC=∠MPB,
∴PM∥BC,
∴OE⊥PM,
∴OE=![]() OP,
OP,
∵PC为⊙O的切线,
∴OC⊥PC,
∴OC=![]() OP,
OP,
∴OE=OC,
而OE⊥PC,
∴PM是⊙O的切线;
(2)在Rt△OPC中,OC=![]() PC=
PC=![]() ,
,
∴四边形OCDB的面积=2S△OCD=2×![]() ×12=
×12=![]() .
.

练习册系列答案
相关题目