题目内容
9.解不等式组$\left\{\begin{array}{l}{x-3(x-2)<4①}\\{\frac{3x+1}{3}≥\frac{x}{2}-1②}\end{array}\right.$,并将解集在数轴上表示出来.分析 解一元一次不等式组的方法与步骤:①求不等式组中每个不等式的解集;②利用数轴求公共部分,据此求出一元一次不等式组的解集,并将解集在数轴上表示出来即可.
解答 解:$\left\{\begin{array}{l}{x-3(x-2)<4①}\\{\frac{3x+1}{3}≥\frac{x}{2}-1②}\end{array}\right.$,
解不等式①,得x>1,
解不等式②,得x≥-$\frac{8}{3}$,
∴这个不等式组的解集是x>1, .
.
点评 此题主要考查了解一元一次不等式组的方法,要熟练掌握,方法与步骤:①求不等式组中每个不等式的解集;②利用数轴求公共部分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知a<b,则下列不等式一定成立的是( )
| A. | a2<ab | B. | ab<b2 | C. | $\frac{3}{2}a>\frac{3}{2}b$ | D. | 7a-7b<0 |
14.整数a( )时,$\frac{|a|-1}{a+1}$的值是-1.
| A. | 为任意整数 | B. | 为任意负整数 | ||
| C. | 等于0或为任意不等于-1的负整数 | D. | 为不等于-1的非正整数 |
18.下列各式计算正确的是( )
| A. | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{3}$ |
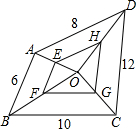 如图,点O为四边形ABCD内任意一点,E,F,G,H分别为边OA,OB,OC,OD的中点,则四边形EFGH的周长=18.
如图,点O为四边形ABCD内任意一点,E,F,G,H分别为边OA,OB,OC,OD的中点,则四边形EFGH的周长=18.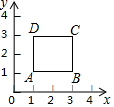 如图,在平面直角坐标系中,点A(1,1),B(3,1),C(3,3),D(1,3),动点P从点A出发,以每秒1个单位长度的速度沿AB-BC-CD-DA-AB-…路线运动,当运动到2017秒时,点P的坐标为(2,1).
如图,在平面直角坐标系中,点A(1,1),B(3,1),C(3,3),D(1,3),动点P从点A出发,以每秒1个单位长度的速度沿AB-BC-CD-DA-AB-…路线运动,当运动到2017秒时,点P的坐标为(2,1). 如图,AB∥CD∥EF,∠B=40°,∠C=105°,则∠CGB=35度.
如图,AB∥CD∥EF,∠B=40°,∠C=105°,则∠CGB=35度. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为3$\sqrt{3}$.
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为3$\sqrt{3}$.