题目内容
7.大地中学八年级为数学竞赛设奖,派了两位老师去学校的超市购买笔记本作为奖品.经过了解得知,超市的A,B两种笔记本的价格分别是10元和6元,他们准备购买这两种笔记本共30本.(1)如果他们购买奖品共花费了240元,则这两种笔记本各买了多少本?
(2)两位老师根据竞赛的设奖情况,决定所购买的A种笔记本的数量要不少于B种笔记本数量,但又不多于B种笔记本数量2倍,如果设他们买A种笔记本n本,买这两种笔记本共花费w元.
①请写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
②请你帮他们计算购买这两种笔记本各多少时,花费最少,此时的花费是多少元?
分析 (1)根据A的本数加B的本数等于总本数,根据A的价格加B的价格等于总价格,可得二元一次方程组,根据解方程组,可得答案;
(2)①根据A的价格加B的价格等于总价格,可得函数解析式,根据A的本数与B的本数的关系,可得自变量的取值范围;
②根据一次函数的性质,可得答案.
解答 解:(1)设购买A中笔记本为x本,购买B中笔记本为y本,由题意,得
$\left\{\begin{array}{l}{x+y=30}\\{10x+6y=240}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=15}\\{y=15}\end{array}\right.$,
答:购买A中笔记本为15本,购买B中笔记本为15本;
(2)①由A的价格加B的价格等于总价格,得
w=10n+6(30-n),
即w=4n+180;
由A种笔记本的数量要不少于B种笔记本数量,但又不多于B种笔记本数量2倍,得
$\left\{\begin{array}{l}{n≥30-n}\\{n≤2(30-n)}\end{array}\right.$,
解得15≤n≤20;
②由w=4n+180,得
k=4>0,
w随n的增加而增加,
当n=15时,w最小=240元,
答:购买A中笔记本为15本,购买B中笔记本为15本,花费最少,此时的花费是240元.
点评 本题考查了一次函数的应用,由题意列出方程组是解题关键,有利用了一次函数的性质:y=kx+b,k>0时,y随x的增大而增大,k<0时,y随x的增大而减小.

练习册系列答案
相关题目
18.下列各式中正确的是( )
| A. | $\sqrt{5}$<2 | B. | -4>-$\sqrt{15}$ | C. | 1-$\sqrt{2}$<0 | D. | $\sqrt{16}$<$\sqrt{8}$ |
16.下列各数中是无理数的是( )
| A. | 8 | B. | $\root{3}{27}$ | C. | $\frac{13}{5}$ | D. | $\sqrt{5}$ |
 如图所示,已知等边三角形ABC的外接圆⊙O的半径为R,求△ABC的边长a、周长P、边心距r及面积S.
如图所示,已知等边三角形ABC的外接圆⊙O的半径为R,求△ABC的边长a、周长P、边心距r及面积S. 分别画出图中几何体的主视图,左视图和俯视图.
分别画出图中几何体的主视图,左视图和俯视图.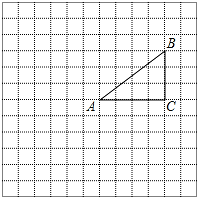 正方形网格中的每个小正方形的边长都是1,顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△A′B′C′.
正方形网格中的每个小正方形的边长都是1,顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△A′B′C′.