题目内容
3.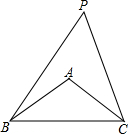 如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=$\frac{1}{2}$∠BAC,求tan∠BPC的值.
如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=$\frac{1}{2}$∠BAC,求tan∠BPC的值.
分析 作AH⊥BC于H,如图,根据等腰三角形的性质得BH=$\frac{1}{2}$BC=4,∠BAH=$\frac{1}{2}$∠BAC,而∠BPC=$\frac{1}{2}$∠BAC,则∠BAH=∠BPC,在Rt△ABH中利用勾股定理计算出AH=3,然后根据正切的定义求解.
解答 解:作AH⊥BC于H,如图,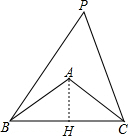
∵AB=AC=5,
∴BH=CH=$\frac{1}{2}$BC=4,AH平分∠BAC,
∴∠BAH=$\frac{1}{2}$∠BAC,
∵∠BPC=$\frac{1}{2}$∠BAC,
∴∠BAH=∠BPC,
在Rt△ABH中,∵AB=5,BH=4,
∴AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=3,
∴tan∠BAH=$\frac{BH}{AH}$=$\frac{4}{3}$,
∴tan∠BPC=$\frac{4}{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解直角三角形要用到的关系:锐角互余的关系、三边之间的关系、边角之间的关系.也考查了等腰三角形的性质.

练习册系列答案
相关题目
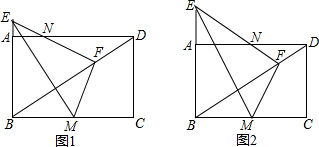
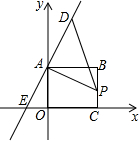 如图,已知四边形ABCD为矩形,O为坐标原点,点A的坐标为(0,6),点C的坐标为(8,0),点P是线段BC上一动点,已知点D是直线AE上位于第一象限的任意一点,直线AE与x轴交于点E(-3,0);
如图,已知四边形ABCD为矩形,O为坐标原点,点A的坐标为(0,6),点C的坐标为(8,0),点P是线段BC上一动点,已知点D是直线AE上位于第一象限的任意一点,直线AE与x轴交于点E(-3,0);