题目内容
11.证明:不论a,b为何值,多项式$-\frac{{{a^2}{b^2}}}{4}$-a2-b2-3ab-5的值一定小于0.分析 利用配方法将多项式$-\frac{{{a^2}{b^2}}}{4}$-a2-b2-3ab-5转化为$-{(\frac{ab}{2}+1)^2}-{({a+b})^2}-4$的形式,然后利用非负数的性质进行论证.
解答 证明:$-\frac{{{a^2}{b^2}}}{4}-{a^2}-{b^2}-3ab-5$,
=$-[(\frac{{{a^2}{b^2}}}{4}+2ab+1)+({a^2}+{b^2}+2ab)+4]$,
=$-{(\frac{ab}{2}+1)^2}-{({a+b})^2}-4$.
∵${(\frac{ab}{2}+1)^2}≥0$,(a+b)2≥0,
∴$-{(\frac{ab}{2}+1)^2}≤0$,-(a+b)2≤0.
∴原式一定小于0.
点评 本题考查了配方法的应用和非负数的性质.解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知点P(4,-3),则P到x轴的距离为( )
| A. | 3 | B. | -3 | C. | 4 | D. | -4 |
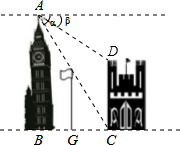 如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.
如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.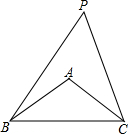 如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=$\frac{1}{2}$∠BAC,求tan∠BPC的值.
如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=$\frac{1}{2}$∠BAC,求tan∠BPC的值.