题目内容
18．如果有2015名学生排成一列，按1，2，3，4，3，2，1，2，3，4，3，2，…的规律报数，那么第2015名学生所报的数是3．分析 首先观察题中数列存在规律：以“1，2，3，4，3，2”6个数循环出现，用2015除以6看余数是多少，进行判断即可．
解答 解：题中数列存在规律：以“1，2，3，4，3，2”6个数循环出现，
2015÷6=335…5，
所以第2015名学生所报的数与第5个学生报的数相同，是3，
故答案为：3．
点评 此题主要考查数列的规律探索与应用，观察已知找出存在的循环出现规律是解题的关键．
练习册系列答案
相关题目
13．若$a=\frac{2003}{2013}，b=\frac{2004}{2014}，c=\frac{2005}{2015}$，则a，b，c的大小关系是（ ）
| A． | c＞b＞a | B． | a＞c＞b | C． | a＞b＞c | D． | c＞a＞b |
3．
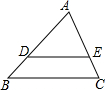如图，在△ABC中，DE∥BC，AD=6，DB=3，则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为（ ）
如图，在△ABC中，DE∥BC，AD=6，DB=3，则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{4}{5}$ | D． | $\frac{4}{9}$ |
18．一次函数y=x+2的图象与x轴的交点坐标是（ ）
| A． | （-2，0） | B． | （2，0） | C． | （0，-2） | D． | （0，2） |