题目内容
13.已知实数x满足方程$\frac{{x}^{2}+2}{x}$-$\frac{3x}{{x}^{2}+2}$=2,则$\frac{{x}^{2}+2}{x}$=3.分析 设则$\frac{{x}^{2}+2}{x}$=y,原方程化为y-$\frac{3}{y}$=2,进而化为整式方程即可求得结论.
解答 解:设则$\frac{{x}^{2}+2}{x}$=y,
原方程化为y-$\frac{3}{y}$=2,
∴y2-2y-3=0,
解得:y1=3,y2=-1,
当y1=3时,$\frac{{x}^{2}+2}{x}$=3,
∴x2-3x+2=0,
∵△=1>0,
∴y1=3符合题意,当y2=-1,$\frac{{x}^{2}+2}{x}$=-1,
∴x2,+x+2=0,
∵△=-71<0,
∴y2=-1不符合题意,
故答案为3.
点评 本题主要考查了换元法解方程,分式方程的解法,能正确设出未知数是解题的关键,同时注意还原为x的方程时,要判别是否有实根.

练习册系列答案
相关题目
1. 如图,点G是△ABC的重心,连接EF交AD于H,则GH:HA是( )
如图,点G是△ABC的重心,连接EF交AD于H,则GH:HA是( )
 如图,点G是△ABC的重心,连接EF交AD于H,则GH:HA是( )
如图,点G是△ABC的重心,连接EF交AD于H,则GH:HA是( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:5 |

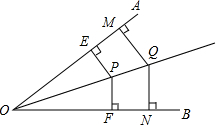 如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.
如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.