题目内容
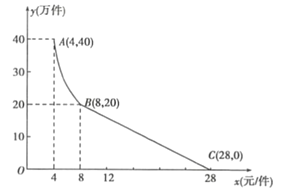
【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图所示的一次函数关系.随着补贴数额的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足![]()
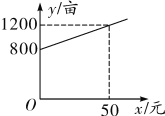
(1)求出政府补贴政策实施后,种植亩数y与政府补贴数额x之间的函数关系式;
(2)在政府出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?求出总收益w的最大值;
(4)该市希望这种蔬菜的总收益不低于7200000元,请你帮助该市确定每亩补贴数额的范围,在此条件下要使总收益最大,并说明每亩补贴数额应定为多少元合适?
参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是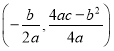 .
.
【答案】(1)![]() ;(2)2400000元;(3)政府应将每亩补贴数额定为450元,总收益w的最大值是7260000元;(4)每亩补贴数额应定为400元到500元最合适
;(2)2400000元;(3)政府应将每亩补贴数额定为450元,总收益w的最大值是7260000元;(4)每亩补贴数额应定为400元到500元最合适
【解析】
(1)设种植亩数y与政府补贴数额x之间的函数关系式是![]() ,
,
由图象过![]() ,将两点代入得:
,将两点代入得:
![]() ,
,
解得:![]() ,
,
∴![]() .
.
答:政府补贴政策实施后,种植亩数y与政府补贴数额x之间的函数关系式是![]() ;
;
(2)![]() ,
,
当![]() 时,
时,![]() ,
,
总收益为![]() 元.
元.
答:在政府出台补贴措施前,该市种植这种蔬菜的总收益额为2400000元;
(3)![]() ,
,
∵![]() ,对称轴
,对称轴![]() ,
,
∴当![]() 时,
时,
![]()
![]() (元),
(元),
∴当x定为450元时,总收益达到最大值,最大值为7260000元.
答:要使全市这种蔬菜的总收益w最大,政府应将每亩补贴数额定为450元,总收益w的最大值是7260000元;
(4)![]() ,
,
∴![]() .
.
因此,定为400元到500元.
答:每亩补贴数额应定为400元到500元最合适.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目