题目内容
1.如果点A(m,n)、B(m+1,n-3)均在一次函数y=kx+b(k≠0)的图象上,那么k的值为-3.分析 直接把两点代入一次函数y=kx+b(k≠0),求出k的值即可.
解答 解:∵点A(m,n)、B(m+1,n-3)均在一次函数y=kx+b(k≠0)的图象上,
∴$\left\{\begin{array}{l}km+b=n\\ k(m+1)+b=n-3\end{array}\right.$,解得k=-3.
故答案为:-3.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
12.为了解我市八年级10000名学生的身高,从中抽取了500名学生,对其身高进行统计分析,以下说法正确的是( )
| A. | 10000名学生是总体 | B. | 本次调查采用的是普查 | ||
| C. | 样本容量是500名学生 | D. | 每个学生的身高是个体 |
6.下列因式分解中正确的是( )
| A. | x2+25=(x+5)(x-5) | B. | 4x2-9y2=(2x+3y)(3x-2y) | ||
| C. | 4x2-6x+1=(2x-3)2 | D. | 2x2-x-6=(x-2)(2x+3) |
11.下列分解因式正确的是( )
| A. | 2x2+4xy=x(2x+4y) | B. | 4a2-4ab+b2=(2a-b)2 | ||
| C. | x3-x=x(x2-1) | D. | 3x2-5xy+x=x(3x-5y) |
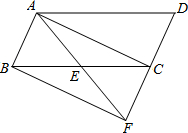 如图,在平行四边形ABCD中,E是BC的中点,连结AE并延长,交DC的延长线于点F.
如图,在平行四边形ABCD中,E是BC的中点,连结AE并延长,交DC的延长线于点F.