题目内容
10. 如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交BC点D,AD平分∠BAC,则∠B度数为30°.
如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交BC点D,AD平分∠BAC,则∠B度数为30°.
分析 根据线段垂直平分线的性质得到DA=DB,得到∠B=∠DAB,根据角平分线的定义得到∠DAB=∠DAC,根据三角形内角和定理计算即可.
解答 解:∵DE是△ABC的AB边的垂直平分线,
∴AD=BD,
∴∠B=∠DAB,
∵AD平分∠BAC,
∴∠DAB=∠DAC,
∴∠B=∠DAB=∠DAC,又∠C=90°,
∴∠B=30°,
故答案为:30°
点评 本题考查了线段垂直平分线性质的应用,能求出∠B=∠DAB=∠DAC是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
20.已知(a+3)2+|b-2|+2=b,则a、b的值是( )
| A. | a=-3,b为任意值 | B. | a=3,b为任意值 | C. | a=-3,b≥2 | D. | 不存在这样的a、b |
18.在直角坐标系中,长方形ABCD的边AB可表示成(2,y)(-1≤y≤3),边BC可表示成(x,3)(2≤x≤5),则点D的坐标是( )
| A. | (5,3) | B. | (5,-1) | C. | (-1,2) | D. | (2,-1) |
15.为了解我区七年级6000名学生期中数学考试情况,从中抽取了500名学生的数学成绩进行统计.下列判断:
①这种调查方式是抽样调查;
②6000名学生是总体;
③每名学生的数学成绩是个体;
④500名学生是总体的一个样本.
其中正确的判断有( )
①这种调查方式是抽样调查;
②6000名学生是总体;
③每名学生的数学成绩是个体;
④500名学生是总体的一个样本.
其中正确的判断有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.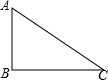 如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
 如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )| A. | 相交 | B. | 相离 | C. | 相切 | D. | 不能确定 |
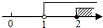
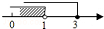

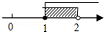
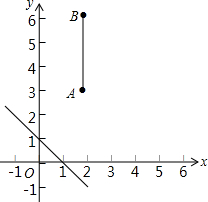 如果,在平面直角坐标系中,已知点A(2,3)、B(2,6),连接AB,如果点P在直线y=-x+1上,且点P到直线的距离小于1,那么点P是线段AB的“环绕点”,若点Q(m,n)是线段AB的“环绕点”,求n的取值范围.
如果,在平面直角坐标系中,已知点A(2,3)、B(2,6),连接AB,如果点P在直线y=-x+1上,且点P到直线的距离小于1,那么点P是线段AB的“环绕点”,若点Q(m,n)是线段AB的“环绕点”,求n的取值范围.