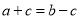题目内容
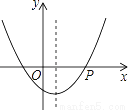
如图,在平面直角坐标系中,O为坐标原点,直线y=﹣x﹣3与x轴交于点A,与y轴交于点C,抛物线y=x2+bx+c经过A、C两点,与x轴交于另一点B
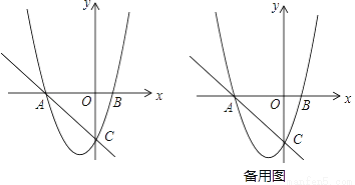
(1)求抛物线的解析式;
(2)点D是第二象限抛物线上的一个动点,连接AD、BD、CD,当S△ACD=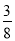 S四边形ACBD时,求D点坐标;
S四边形ACBD时,求D点坐标;
(3)在(2)的条件下,连接BC,过点D作DE⊥BC,交CB的延长线于点E,点P是第三象限抛物线上的一个动点,点P关于点B的对称点为点Q,连接QE,延长QE与抛物线在A、D之间的部分交于一点F,当∠DEF+∠BPC=∠DBE时,求EF的长.
(1)y=x2+2x﹣3(2)(﹣4,5)(3)3+ 【解析】试题分析:(1)、首先求出点A和点C的坐标,然后将其代入二次函数解析式,利用待定系数法求出函数解析式;(2)、首先求出AB的长度,然后根据面积之间的关系得出点E的坐标,从而得出直线CE的函数解析式,将一次函数和二次函数联立成方程组,从而得出点D的坐标;(3)、过点D作DN⊥x轴,垂足为N,过点P作PM⊥x轴,垂足为M,利用待定系数...
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:则当2<y<5时,x的取值范围是________
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 10 | 5 | 2 | 1 | 2 | … |


 ,则此三角形移动的距离AA′是( )
,则此三角形移动的距离AA′是( )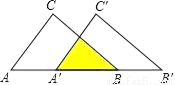
 -1 B.
-1 B. 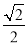 C. 1 D.
C. 1 D. 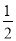
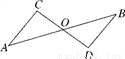
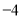 ______
______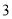 (用“>”,“<”或“=”填空).
(用“>”,“<”或“=”填空).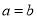 ,那么
,那么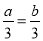 B. 如果
B. 如果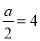 ,那么
,那么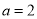
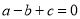 ,那么
,那么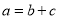 D. 如果
D. 如果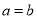 ,那么
,那么