题目内容
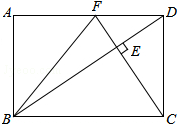 在矩形ABCD中,CF⊥BD分别交BD、AD于点E、F,连接BF.
在矩形ABCD中,CF⊥BD分别交BD、AD于点E、F,连接BF.(1)求证:△DEC∽△FDC;
(2)若DE=2
| 3 |
考点:相似三角形的判定与性质
专题:
分析:(1)由矩形的性质可知∠FDC=∠DEC=90°,结合公共角可证明△DEC∽△FDC;
(2)由DF∥BC可知
=
=
,可求得BE,进一步可求出BD.
(2)由DF∥BC可知
| DE |
| BE |
| DF |
| BC |
| 1 |
| 2 |
解答:(1)证明:∵四边形ABCD为矩形,CF⊥BD,
∴∠FDC=∠DEC=90°,且∠DCE=∠DCF,
∴△DEC∽△FDC;
(2)解:∵四边形ABCD为矩形,
∴DF∥BC,且F为中点,
∴
=
=
,且DE=2
,
∴BE=4
,
∴BD=BE+DE=4
+2
=6
.
∴∠FDC=∠DEC=90°,且∠DCE=∠DCF,
∴△DEC∽△FDC;
(2)解:∵四边形ABCD为矩形,
∴DF∥BC,且F为中点,
∴
| DE |
| BE |
| DF |
| BC |
| 1 |
| 2 |
| 3 |
∴BE=4
| 3 |
∴BD=BE+DE=4
| 3 |
| 3 |
| 3 |
点评:本题主要考查相似三角形的判定及平行线分线段成比例,掌握相似三角形的判定方法是解题的关键.

练习册系列答案
相关题目
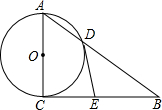 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,E为BC的中点,连接DE.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,E为BC的中点,连接DE.