题目内容
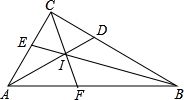 如图,在△ABC中,∠ACB=90°,角平分线BE、AD相交于I,连结CI并延长交AB于点F,则下列结论中错误的是( )
如图,在△ABC中,∠ACB=90°,角平分线BE、AD相交于I,连结CI并延长交AB于点F,则下列结论中错误的是( )| A、点I在∠ABC的平分线上 |
| B、点F在∠AIB的平分线上 |
| C、∠ACI=45° |
| D、∠CAD+∠ABE+∠BCF=90° |
考点:角平分线的性质
专题:
分析:由BE平分∠ABC可判断A正确;
由在△ABC中,角平分线BE、AD相交于I,根据角平分线的性质与判定可得CI平分∠ACB,再根据三角形外角的性质及∠CAB≠∠ABC,可判断B错误;
由∠ACB=90°,CI平分∠ACB可判断C正确;
由三角形内角和定理及角平分线定义可判断D正确.
由在△ABC中,角平分线BE、AD相交于I,根据角平分线的性质与判定可得CI平分∠ACB,再根据三角形外角的性质及∠CAB≠∠ABC,可判断B错误;
由∠ACB=90°,CI平分∠ACB可判断C正确;
由三角形内角和定理及角平分线定义可判断D正确.
解答: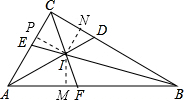 解:A、∵在△ABC中,角平分线BE、AD相交于I,
解:A、∵在△ABC中,角平分线BE、AD相交于I,
∴点I在∠ABC的平分线上,故本选项正确;
B、过I点分别作AB、BC、AC的垂线,垂足分别为M、N、P,
∵在△ABC中,角平分线BE、AD相交于I,
∴IM=IN,IM=IP,
∴IN=IP,
∴CF平分∠ACB,∠ACF=∠BCF.
∵∠AIF=∠ACI+∠CAI,∠BIF=∠BCI+∠CBI,
∠ACI=∠BCI,∠CAI≠∠CBI,
∴∠AIF≠∠BIF,
∴点F不在∠AIB的平分线上,故本选项错误;
C、∵∠ACB=90°,CI平分∠ACB,
∴∠ACI=
∠ACB=45°,故本选项正确;
D、∵BE、AD、CF是△ABC的角平分线,
∴∠CAD=
∠BAC,∠ABE=
∠ABC,∠BCF=
∠ACB,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠CAD+∠ABE+∠BCF=
(∠BAC+∠ABC+∠ACB)=90°,故本选项正确.
故选B.
 解:A、∵在△ABC中,角平分线BE、AD相交于I,
解:A、∵在△ABC中,角平分线BE、AD相交于I,∴点I在∠ABC的平分线上,故本选项正确;
B、过I点分别作AB、BC、AC的垂线,垂足分别为M、N、P,
∵在△ABC中,角平分线BE、AD相交于I,
∴IM=IN,IM=IP,
∴IN=IP,
∴CF平分∠ACB,∠ACF=∠BCF.
∵∠AIF=∠ACI+∠CAI,∠BIF=∠BCI+∠CBI,
∠ACI=∠BCI,∠CAI≠∠CBI,
∴∠AIF≠∠BIF,
∴点F不在∠AIB的平分线上,故本选项错误;
C、∵∠ACB=90°,CI平分∠ACB,
∴∠ACI=
| 1 |
| 2 |
D、∵BE、AD、CF是△ABC的角平分线,
∴∠CAD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BAC+∠ABC+∠ACB=180°,
∴∠CAD+∠ABE+∠BCF=
| 1 |
| 2 |
故选B.
点评:本题考查的是角平分线的性质及判定定理,角平分线上的点到角两边的距离相等;到一个角的两边距离相等的点在这个角的角平分线上.也考查了三角形内角和定理及外角的性质.

练习册系列答案
相关题目
 已知线段a,b,∠α,求作:△ABC,AB=a,AC=b,∠BAC=∠α
已知线段a,b,∠α,求作:△ABC,AB=a,AC=b,∠BAC=∠α 如图,是屋架设计图的一部分,点D时斜梁AB的中点,立柱BC、DE垂直于横架AC,AB=7.4m,∠A=30°,立柱BC、DE需要多长?
如图,是屋架设计图的一部分,点D时斜梁AB的中点,立柱BC、DE垂直于横架AC,AB=7.4m,∠A=30°,立柱BC、DE需要多长? 在5×5的正方形网格中,每个小格的边长均为1,把顶点是格点(即正方形的顶点)的四边形称为格点四边形.
在5×5的正方形网格中,每个小格的边长均为1,把顶点是格点(即正方形的顶点)的四边形称为格点四边形. 如图,⊙O的直径AB和弦CD相交于点E.∠DEB=60°,AE=1,EB=5.试求CD的长.
如图,⊙O的直径AB和弦CD相交于点E.∠DEB=60°,AE=1,EB=5.试求CD的长.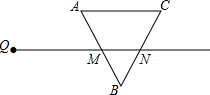 射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,
射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,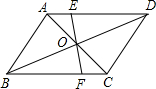 如图,平行四边形ABCD的对角线AC、BD相交于点O,过点O作直线分别交AD、BC于点E、F,如果四边形AEFB的面积为8,则平行四边形ABCD的面积是
如图,平行四边形ABCD的对角线AC、BD相交于点O,过点O作直线分别交AD、BC于点E、F,如果四边形AEFB的面积为8,则平行四边形ABCD的面积是 如图,在△ABC中,∠B=∠C,D为边BC上一点,E为AC上一点,∠BAD=50°,∠ADE=∠AED,求∠EDC的度数.
如图,在△ABC中,∠B=∠C,D为边BC上一点,E为AC上一点,∠BAD=50°,∠ADE=∠AED,求∠EDC的度数.