题目内容
7.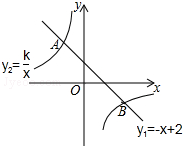 如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,点B的坐标为(2m,-m).
如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,点B的坐标为(2m,-m).(1)求出m值并确定反比例函数的表达式;
(2)请直接写出当x<m时,y2的取值范围.
分析 (1)把B的坐标代入y1=-x+2求得m的值,得出B(4,-2),再代入入y2=$\frac{k}{x}$即可求得k的值;
(2)根据图象即可求得.
解答 解:(1)∵据题意,点B的坐标为(2m,-m)且在一次函数y1=-x+2的图象上,代入得-m=-2m+2.
∴m=2.
∴B点坐标为(4,-2),
把B(4,-2)代入y2=$\frac{k}{x}$得k=4×(-2)=-8,
∴反比例函数表达式为y2=-$\frac{8}{x}$;
(2)当x<4,y2的取值范围为y2>0或y2<-2.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
相关题目
19.已知点A,C在直线BD的同侧,且AB⊥BD于B,CD⊥BD于D,AB=6,CD=4,BD=14,现有点P在直线BD上,并且满足△ABP与△CDP相似,则这样的点P的个数为( )
| A. | 3 | B. | 5 | C. | 6 | D. | 7 |
12.分别数一数四棱锥、五棱锥、六棱锥和八棱锥的顶点数、面数和棱数,填写下表,你发现了什么规律?
你发现的规律是顶点数+面数-棱数=2.
| 顶点数 | 面数 | 棱数 | 顶点数+面数-棱数 | |
| 四棱锥 | 5 | 5 | 8 | 2 |
| 五棱锥 | 6 | 6 | 10 | 2 |
| 六棱锥 | 7 | 7 | 12 | 2 |
| 八棱锥 | 9 | 9 | 16 | 2 |
