题目内容
以长为2的线段AB为边作正方形ABCD,取AB的中点P,连结PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上,如图.

求AM、DM的长.
求证:AM2=AD·DM.
根据的结论你能找出图中的黄金分割点吗?
答案:
解析:
提示:
解析:
|
如图:
∴ AB=AD=2,AP=1在 Rt△APD中,PD=
∵ PF=PD,∴ AF=PF-AP= -1 -1
∵ AMEF是正方形,∴ AM=AF= -1 -1
DM =AD-AM=2-( -1)=3- -1)=3- 证明:由得AM2=
证明:由得AM2= =6-2 =6-2
AD ·DM=2(3- )=6-2 )=6-2
∴ AM2=AD·DM由知图中点M是线段AD的黄金分割点. |
提示:
|
正确理解题意,分析已知和未知,合理作答. |

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
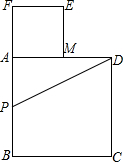 如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,
如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上,则AM的长为( )
A、
| ||||
B、
| ||||
C、3-
| ||||
D、6-2
|

 以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.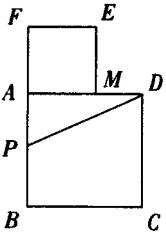
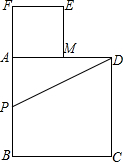 如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,
如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F, -1
-1
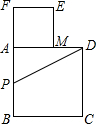 以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.