题目内容
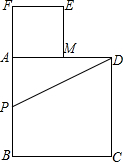 如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,
如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,
使PF=PD,以AF为边作正方形AMEF,点M在AD上,则AM的长为
- A.
 -1
-1 - B.

- C.3-

- D.6-2

A
分析:要求AM的长,只需求得AF的长,根据AF、AP和PF之间的关系,可得出AF的长度,又AF=AM,即可得出.
解答:在Rt△APD中,AP=1,AD=2,
由勾股定理知PD= =
= =
= ,
,
∴AM=AF=PF-AP=PD-AP= -1.
-1.
故选A.
点评:此题综合运用了正方形的性质和勾股定理.
分析:要求AM的长,只需求得AF的长,根据AF、AP和PF之间的关系,可得出AF的长度,又AF=AM,即可得出.
解答:在Rt△APD中,AP=1,AD=2,
由勾股定理知PD=
 =
= =
= ,
,∴AM=AF=PF-AP=PD-AP=
 -1.
-1.故选A.
点评:此题综合运用了正方形的性质和勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
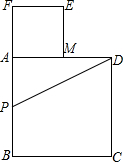 如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,
如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上,则AM的长为( )
A、
| ||||
B、
| ||||
C、3-
| ||||
D、6-2
|
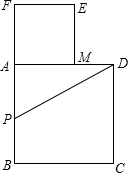 F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.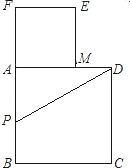 如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
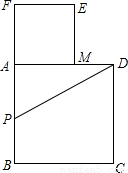 F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.