题目内容
随着人们经济收入的提高及汽车产业的快速发展,汽车已经越来越多进入普通家庭,成为居民消费新的增长点,据某市交通部门统计,2011年底全是汽车拥有量为15万辆,而截止到2013年底全市汽车拥有量已达到21.6万辆.
(1)求2011年底到2013年底该市汽车拥有量的年平均增长率;
(2)为了保护环境,缓解汽车拥堵情况,从2014年起,该市交通部分拟控制汽车总量,要求到2015年底全市汽车拥有量不超过23.196万辆;另据统计,该市从2014年起每年报废的汽车数量是上年底汽车拥有量的10%,假定在这种情况下每年汽车新增数量相同,请你计算出该市每年新增汽车数量最多不能超过多少万辆.
(1)求2011年底到2013年底该市汽车拥有量的年平均增长率;
(2)为了保护环境,缓解汽车拥堵情况,从2014年起,该市交通部分拟控制汽车总量,要求到2015年底全市汽车拥有量不超过23.196万辆;另据统计,该市从2014年起每年报废的汽车数量是上年底汽车拥有量的10%,假定在这种情况下每年汽车新增数量相同,请你计算出该市每年新增汽车数量最多不能超过多少万辆.
考点:一元二次方程的应用,一元一次不等式的应用
专题:
分析:(1)设该市汽车拥有量的年平均增长率为x,根据题意列出方程,不合题意的解,舍去即可;
(2)设全市每年新增汽车数量为y万辆,则得出2014年底和2015年底全市的汽车拥有量,从而列出不等式求解即可.
(2)设全市每年新增汽车数量为y万辆,则得出2014年底和2015年底全市的汽车拥有量,从而列出不等式求解即可.
解答:解:(1)设该市汽车拥有量的年平均增长率为x,
根据题意得,15(1+x)2=21.6,
解得x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:该市汽车拥有量的年平均增长率为20%;
(2)设全市每年新增汽车数量为y万辆,
则2014年底全市的汽车拥有量为[21.6×(1-10%)+y]万辆,
2015年底全市的汽车拥有量为[21.6×(1-10%)+y]×(1-10%)+y万辆.
根据题意得:[21.6×(1-10%)+y]×(1-10%)+y≤23.196,
解得y≤3.
答:该市每年新增汽车数量最多不能超过3万辆.
根据题意得,15(1+x)2=21.6,
解得x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:该市汽车拥有量的年平均增长率为20%;
(2)设全市每年新增汽车数量为y万辆,
则2014年底全市的汽车拥有量为[21.6×(1-10%)+y]万辆,
2015年底全市的汽车拥有量为[21.6×(1-10%)+y]×(1-10%)+y万辆.
根据题意得:[21.6×(1-10%)+y]×(1-10%)+y≤23.196,
解得y≤3.
答:该市每年新增汽车数量最多不能超过3万辆.
点评:本题考查了一元二次方程和不等式的应用,判断所求的解是否符合题意,舍去不合题意的解.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
甲班有学生50人,乙班有学生45人,要使甲班人数是乙班人数的2倍,应从乙班调多少学生到甲班?设从乙班调出x人,则可列出的方程是( )
A、
| ||
| B、50-x=2(45+x) | ||
| C、50+2x=45 | ||
| D、50+x=2(45-x) |
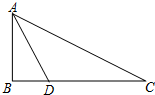 如图,△ABC中,∠B=90°,BC=8,BC上一点D,使BD:CD=3:5.
如图,△ABC中,∠B=90°,BC=8,BC上一点D,使BD:CD=3:5.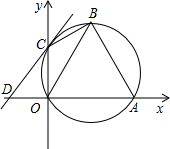 如图,直角坐标系中,已知两点O(0,0),A(2,0),点B在第一象限且△OAB为正三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.
如图,直角坐标系中,已知两点O(0,0),A(2,0),点B在第一象限且△OAB为正三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.