题目内容
4. 如图,点G在平行四边形ABCD的边DC的延长线上,AG交BC、BD于E、F,求证:AF2=EF•FG.
如图,点G在平行四边形ABCD的边DC的延长线上,AG交BC、BD于E、F,求证:AF2=EF•FG.
分析 由四边形ABCD是平行四边形可得AB∥DC,AD∥BC,从而可得△GDF∽△ABF,△AFD∽△EFB,则有$\frac{FD}{FB}$=$\frac{FG}{FA}$,$\frac{AF}{EF}$=$\frac{FD}{FB}$,就有$\frac{FG}{FA}$=$\frac{AF}{EF}$,即AF2=EF•FG.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,
∴△GDF∽△ABF,△AFD∽△EFB,
∴$\frac{FD}{FB}$=$\frac{FG}{FA}$,$\frac{AF}{EF}$=$\frac{FD}{FB}$,
∴$\frac{FG}{FA}$=$\frac{AF}{EF}$,
∴AF2=EF•FG.
点评 本题主要考查了平行四边形的性质、相似三角形的判定与性质、等量代换等知识,把证明$\frac{FG}{FA}$=$\frac{AF}{EF}$转化为证明$\frac{FD}{FB}$=$\frac{FG}{FA}$,$\frac{AF}{EF}$=$\frac{FD}{FB}$是解决本题的关键.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
16.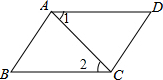 如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
 如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )| A. | AB=DC | B. | ∠1=∠2 | C. | AB=AD | D. | ∠D=∠B |
13.【问题提出】用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
【问题探究】不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以先从特殊入手,通过试验、观察、类比、最后归纳、猜测得出结论.
【探究一】
(1)用3根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
此时,显然能搭成一种等腰三角形.
所以,当n=3时,m=1.
(2)用4根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形.
所以,当n=4时,m=0.
(3)用5根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形.
所以,当n=5时,m=1.
(4)用6根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形.
所以,当n=6时,m=1.
综上所述,可得:表①
【探究二】
(1)用7根相同的木棒搭一个三角形,能搭成多少种不同的三角形?
(仿照上述探究方法,写出解答过程,并将结果填在表②中)
(2)用8根、9根、10根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
表②
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
【问题解决】:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(设n分别等于4k-1,4k,4k+1,4k+2,其中k是正整数,把结果填在表③中)
表③
【问题应用】:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(写出解答过程),其中面积最大的等腰三角形每腰用了672根木棒.(只填结果)
【问题探究】不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以先从特殊入手,通过试验、观察、类比、最后归纳、猜测得出结论.
【探究一】
(1)用3根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
此时,显然能搭成一种等腰三角形.
所以,当n=3时,m=1.
(2)用4根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形.
所以,当n=4时,m=0.
(3)用5根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形.
所以,当n=5时,m=1.
(4)用6根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形.
所以,当n=6时,m=1.
综上所述,可得:表①
| n | 3 | 4 | 5 | 6 |
| m | 1 | 0 | 1 | 1 |
(1)用7根相同的木棒搭一个三角形,能搭成多少种不同的三角形?
(仿照上述探究方法,写出解答过程,并将结果填在表②中)
(2)用8根、9根、10根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
表②
| n | 7 | 8 | 9 | 10 |
| m | 2 | 1 | 2 | 2 |
【问题解决】:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(设n分别等于4k-1,4k,4k+1,4k+2,其中k是正整数,把结果填在表③中)
表③
| n | 4k-1 | 4k | 4k+1 | 4k+2 |
| m | k | k-1 | k | k |
14.2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为( )
| A. | 3×106 | B. | 3×105 | C. | 0.3×106 | D. | 30×104 |
 (1)画出图中的10块小立方块搭成几何体的主视图、左视图和俯视图.
(1)画出图中的10块小立方块搭成几何体的主视图、左视图和俯视图.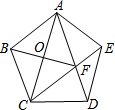 如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2.
如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2.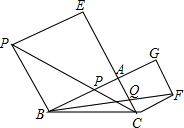 如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.
如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.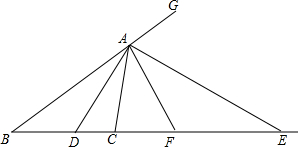 如图,已知△ABC中,AD,AE分别是∠CAB及其外角平分线,分别交CB及CB的延长线于D、E,F为DE的中点,求证:
如图,已知△ABC中,AD,AE分别是∠CAB及其外角平分线,分别交CB及CB的延长线于D、E,F为DE的中点,求证: