题目内容
9.学校组织“中华经典诗词大赛”,共设有20个试题,其中有关“诗句理解”的试题10个,有关“诗句作者”的试题6个,有关“诗句默写”的试题4个,小杰从中任选一个试题作答,他选中有关“诗句作者”的试题的概率是$\frac{3}{10}$.分析 根据共设有20道试题,其中有关“诗句作者”的试题6个,再根据概率公式即可得出答案.
解答 解:∵共设有20个试题,其中有关“诗句理解”的试题10个,有关“诗句作者”的试题6个,有关“诗句默写”的试题4个,
∴小杰从中任选一个试题作答,他选中有关“诗句作者”的试题的概率是:$\frac{6}{20}$=$\frac{3}{10}$.
故答案为:$\frac{3}{10}$.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
19. 如图是由6个相同的小正方体组成的立体图形,其主视图是( )
如图是由6个相同的小正方体组成的立体图形,其主视图是( )
 如图是由6个相同的小正方体组成的立体图形,其主视图是( )
如图是由6个相同的小正方体组成的立体图形,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
20.小华通过学习函数发现:若二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,y1),(x2,y2)(x1<x2),若y1y2<0,则方程ax2+bx+c=0(a≠0)的一个根x0的取值范围是x1<x0<x2,请你类比此方法,推断方程x3+x-1=0的实数根x0所在范围为( )
| A. | -$\frac{1}{2}$<x0<0 | B. | 0<x0<$\frac{1}{2}$ | C. | $\frac{1}{2}$<x0<1 | D. | 1<x0<$\frac{3}{2}$ |
17.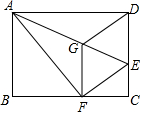 如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
①∠ADG=∠AFG;②四边形DEFG是菱形;③DG2=$\frac{1}{2}$AE•EG;④若AB=4,AD=5,则CE=1.
 如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )①∠ADG=∠AFG;②四边形DEFG是菱形;③DG2=$\frac{1}{2}$AE•EG;④若AB=4,AD=5,则CE=1.
| A. | ①②③④ | B. | ①②③ | C. | ①③④ | D. | ①② |
14.通常在频率分布直方图中,用每小组对应的小矩形的面积表示该小组的组频率.因此,频率分布直方图的纵轴表示( )
| A. | $\frac{频数}{组距}$ | B. | $\frac{频率}{组距}$ | C. | $\frac{频率}{组数}$ | D. | $\frac{频数}{组数}$ |
1.已知关于x的一元二次方程mx2+2x-1=0有两实数根,则m的取值范围是( )
| A. | m>1 | B. | m≥-1 | C. | m>-1且m≠0 | D. | m≥-1且m≠0 |
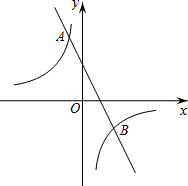 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).