题目内容
20.等腰三角形的腰长为5,底边长为6,则它底边上的高为4.分析 根据等腰三角形底边高线和中线重合的性质,则BD=DC=3,可以根据勾股定理计算底边的高AD=$\sqrt{A{B}^{2}-B{D}^{2}}$.
解答  解:如图,在△ABC中,AB=AC=5,AD⊥BC,
解:如图,在△ABC中,AB=AC=5,AD⊥BC,
则AD为BC边上的中线,即D为BC中点,
∴BD=DC=3,
在直角△ABD中AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=4.
故答案为:4.
点评 本题考查了勾股定理在直角三角形中的正确运用,考查了等腰三角形底边高线、中线重合的性质,本题中根据勾股定理正确计算AD是解题的关键.

练习册系列答案
相关题目
10.下列方程是二元一次方程的是( )
| A. | x+$\frac{1}{y}$=1 | B. | 2x+3y=6 | C. | x2-y=3 | D. | 3x-5(x+2)=2 |
11.商品原价389元,经连续两次降价后售价为279元,设平均每降价的百分率为x,则下面所列方程正确的是( )
| A. | 389(1-x)2=279 | B. | 279(1-x)2=389 | C. | 389(1-2x)=279 | D. | 279(1-2x)=389 |
15.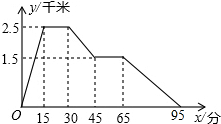 图象中所反映的过程是:小敏从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )
图象中所反映的过程是:小敏从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )
 图象中所反映的过程是:小敏从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )
图象中所反映的过程是:小敏从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )| A. | 体育场离小敏家2.5千米 | B. | 体育场离早餐店4千米 | ||
| C. | 小敏在体育场锻炼了15分钟 | D. | 小敏从早餐店回到家用时30分钟 |
9.符合下列条件的四边形不一定是菱形的是( )
| A. | 四边都相等 | B. | 两组邻边分别相等 | ||
| C. | 对角线互相垂直平分 | D. | 两条对角线分别平分一组对角 |
 如图,求∠FAC+∠B+∠C+∠BDE+∠E+∠F的度数.
如图,求∠FAC+∠B+∠C+∠BDE+∠E+∠F的度数.