题目内容
5．解方程：$\frac{a-b}{a+2b}$÷$\frac{{{a^2}-{b^2}}}{{{a^2}+4ab+4{b^2}}}$-1，其中a=3+$\sqrt{5}$，b=3-$\sqrt{5}$．分析 原式根据分式的除法公式化成乘法，然后化简，最后算减法，把a=3+$\sqrt{5}$，b=3-$\sqrt{5}$代入求得即可．
解答 解：原式=$\frac{a-b}{a+2b}$•$\frac{（a+2b）^{2}}{（a+b）（a-b）}$-1=$\frac{a+2b}{a+b}$-$\frac{a+b}{a+b}$=$\frac{b}{a+b}$；
当$a=3+\sqrt{5}$，$b=3-\sqrt{5}$时，原式=$\frac{{3-\sqrt{5}}}{6}$．
点评 本题考查了分式的化简求值，熟练掌握分式的运算法则时解题的关键．
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
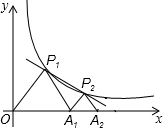如图，P1、P2（P2在P1的右侧）是y=$\frac{k}{x}$（k＞0）在第一象限上的两点，点A1的坐标为（2，0）．
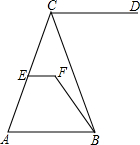如图，EF∥AB，∠DCB=80°，∠CBF=20°，∠EFB=120°，判断直线CD与AB有怎样的位置关系，并说明理由．
如图，∠AOB=120°，∠BOD=90°，OC平分∠BOD，求∠AOC的度数．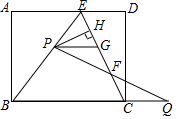
如图，在矩形ABCD中，E是AD上一点，AB=8，BE=BC=10，动点P在线段BE上（与点B、E不重合），点Q在BC的延长线上，PE=CQ，PQ交EC于点F，PG∥BQ交EC于点G，设PE=x．
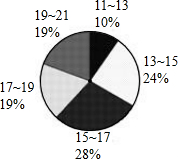某大型网店为了对网上促销员建立销售业绩管理制度，随机抽取了部分促销员，统计了他们的月平均销售业绩（单位：万元），制作了如图的扇形统计图．如果要使半数左右的促销员都能达到业绩目标，则每个促销员最合适的月销售额目标应该定为16万左右．（结果取整数）
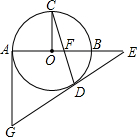如图，AB为⊙O直径，C是⊙O上一点，CO⊥AB于点O，弦CD与AB交于点F，过点D作∠CDE=∠DFE，DE交AB的延长线于点E，过点A作⊙O的切线交ED的延长线于点G．