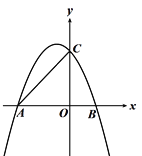题目内容
【题目】在平面直角坐标系中,已知正方形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 在第一象限内,抛物线
在第一象限内,抛物线![]() (
(![]() 常数)的顶点
常数)的顶点![]() 为正方形对角线
为正方形对角线![]() 上一动点.
上一动点.
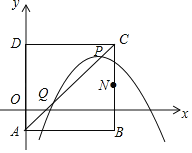
(1)当抛物线经过![]() 两点时,求抛物线的解析式;
两点时,求抛物线的解析式;
(2)若抛物线与直线![]() 相交于另一点
相交于另一点![]() (
(![]() 非抛物线顶点,且
非抛物线顶点,且![]() 在第一象限内),求证:
在第一象限内),求证:![]() 长是定值;
长是定值;
(3)根据(2)的结论,取![]() 的中点
的中点![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)抛物线解析式为![]() ;
;
(2)证明见解析;
(3)最小值为![]() .
.
【解析】
(1)把![]() 点和
点和![]() 点坐标代入
点坐标代入![]() 得到关于
得到关于![]() 的方程组,然后解方程组即可;
的方程组,然后解方程组即可;
(2)先利用正方形性质得到![]() ,再利用待定系数法求出直线
,再利用待定系数法求出直线![]() 的解析式为
的解析式为![]() ,再求出顶点
,再求出顶点![]() 的坐标为
的坐标为![]() ,然后把
,然后把![]() 代入
代入![]() 得到
得到![]() ,设
,设![]() ,
,![]() ,则
,则![]() 为
为![]() 的两根,利用根与系数的关系得到
的两根,利用根与系数的关系得到![]() ,
,![]() ,然后利用两点间的距离公式计算
,然后利用两点间的距离公式计算![]()
![]()
![]()
![]() ,从而判定
,从而判定![]() 长是定值;
长是定值;
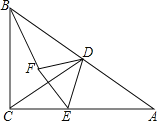
(3)取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,如图,则
,如图,则![]() ,
,![]() ,则过
,则过![]() 点作
点作![]() 的平行线交
的平行线交![]() 于
于![]() ,利用四边形
,利用四边形![]() 为平行四边形得到
为平行四边形得到![]() ,所以
,所以![]()
![]() ,利用两点之间线段最短判断此时
,利用两点之间线段最短判断此时![]() 的值最小,利用勾股定理可计算出它的最小值.
的值最小,利用勾股定理可计算出它的最小值.
(1)解:把![]() ,
,![]() 代入
代入![]()
得![]() ,解得
,解得![]() ,
,
所以抛物线解析式为![]() ;
;
(2)证明:![]() 四边形
四边形![]() 为正方形,
为正方形,
而![]() ,
,
![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() ,
,![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
![]()
![]() ,
,
![]() 顶点
顶点![]() 的坐标为
的坐标为![]() ,
,
把![]() 代入
代入![]() 得
得![]() 的坐标
的坐标![]() ,
,
即![]() ,
,
设![]() ,
,![]() ,
,
则![]() 为
为![]() 的两根,
的两根,
整理为![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]() ,
,
即![]() 长是定值;
长是定值;
(3)取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,如图,
,如图,
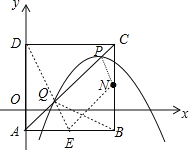
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 过
过![]() 点作
点作![]() 的平行线交
的平行线交![]() 于
于![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
![]() ,
,
![]()
![]() ,
,
此时![]() 的值最小,最小值为
的值最小,最小值为![]() .
.

【题目】小张同学尝试运用课堂上学到的方法,自主研究函数y=![]() 的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
(1)函数y=![]() 自变量的取值范围是 ;
自变量的取值范围是 ;
(2)下表列出了y与x的几组对应值:
x | … | ﹣2 | ﹣ | m | ﹣ | ﹣ |
|
| 1 |
| 2 | … |
y | … |
|
| 1 |
| 4 | 4 |
| 1 |
|
| … |
表中m的值是 ;
(3)如图,在平面直角坐标系xOy中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图象;
(4)结合函数y=![]() 的图象,写出这个函数的性质: .(只需写一个)
的图象,写出这个函数的性质: .(只需写一个)