题目内容
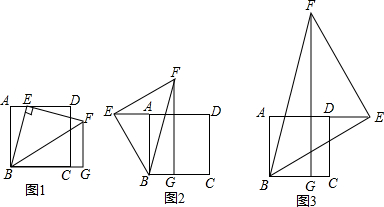
10.已知正方形ABCD,点E在直线AD上(不与点A、D重合),连接BE,做EF⊥BE,且EF=BE,过点F作FG⊥BC,交直线BC于点G.(1)当点E在边AD上,点G在边BC的延长线上时,如图1,求证:AB+AE=BG;
(2)当点E在边DA的延长线上,点G在边BC上时,如图2,试猜想AB、AE与BG的关系,并加以证明;
(3)当点E在边AD的延长线上,点G在边BC上时,如图3,请直接写出线段AB,AE,BG之间的数量关系,不需要证明.
分析 (1)延长AD交GF的延长线于M,根据正方形的性质和全等三角形的判定定理证明△ABE≌△MEF,得到AB=EM,证明结论;
(2)证明△ABE≌△HEF,得到AB=EH,证明结论;
(3)证明△ABE≌△NEF,得到AB=EN,证明结论.
解答 (1)证明:延长AD交GF的延长线于M,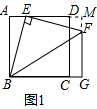
∵四边形ABCD是正方形,
∴∠A=90°,∠ABC=90°,又FG⊥BC,
∴四边形ABGM是矩形,
∴AM=BG,
∵∠A=90°,EF⊥BE,∠M=90°,
∴∠AEB=∠MFE,
在△ABE和△MEF中,
$\left\{\begin{array}{l}{∠A=∠M}\\{∠AEB=∠MFE}\\{EB=EF}\end{array}\right.$,
∴△ABE≌△MEF,
∴AB=EM,
∵AM=AE+EM=AE+AB,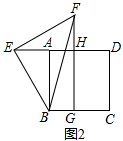
∴AB+AE=BG;
(2)AB-AE=BG.
证明:∵∠FEH+∠BEA=90°,∠BEA+∠ABE=90°,
∴∠FEH=∠ABE,
在△ABE和△HEF中,
$\left\{\begin{array}{l}{∠BAE=∠EHF}\\{∠ABE=∠HEF}\\{EB=EF}\end{array}\right.$,
∴△ABE≌△HEF,
∴EH=AB,
EH-AE═AB-AE=AH,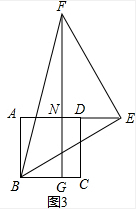
∵四边形ABGH是矩形,
∴AH=BG,
∴AB-AE=BG;
(3)AE=AB+BG.
证明:由(2)得,△ABE≌△NEF,
∴NE=AB,
∵AN+NE=AN+AB=AE,BG=AN,
∴AE=AB+BG.
点评 本题考查的是正方形的性质、矩形的判定和性质、全等三角形的判定和性质,掌握正方形的性质定理、全等三角形的判定定理和性质定理是解题的关键,注意类比思想在解题中的灵活运用.

练习册系列答案
相关题目
5.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a2+a3=a5 | C. | (a2)3=a6 | D. | (-2x)3=-6x3 |
15. 如图,数轴上表示的是两个不等式的解集,由它们组成的不等式组的解集为( )
如图,数轴上表示的是两个不等式的解集,由它们组成的不等式组的解集为( )
 如图,数轴上表示的是两个不等式的解集,由它们组成的不等式组的解集为( )
如图,数轴上表示的是两个不等式的解集,由它们组成的不等式组的解集为( )| A. | -1<x≤1 | B. | -1<x<1 | C. | x>-1 | D. | x≤1 |
19.某商场为了促销,凡购买1000元商品的顾客获抽奖券一张.抽奖活动设置了如下的电翻奖牌,一张抽奖券只能有一次机会在9个数字中选中一个翻牌,其对应的反面就是奖品(重新启动会自动随机交换位置).
(1)求一张抽奖券翻到一台电风扇的概率;
(2)有两张抽奖券翻奖牌,请你根据题意写出一个事件,使这个事件发生的概率是$\frac{1}{9}$.
翻奖牌正面
翻奖牌反面.
(1)求一张抽奖券翻到一台电风扇的概率;
(2)有两张抽奖券翻奖牌,请你根据题意写出一个事件,使这个事件发生的概率是$\frac{1}{9}$.
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 一台电风扇 | 一台收音机 | 谢谢参与 |
| 谢谢参与 | 一副球拍 | 一个U盘 |
| 两张电影票 | 谢谢参与 | 一副球拍 |
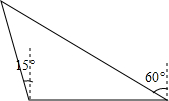 如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离.
如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离. 如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有4种拼接方法.
如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有4种拼接方法.