题目内容
某商店将进货为10元的商品按每件12元售出,每天可销售100件,现在采用提高商品售价减少销售量的办法增加利润,如果这种商品按每件的销售价每提高2元其销售量就减少20件,问应将每件售价定为多少元时,才能使每天利润为320元?
考点:一元二次方程的应用
专题:销售问题
分析:设售价为x元,则有(x-进价)(每天售出的数量-
×20)=每天利润,解方程求解即可.
| x-12 |
| 2 |
解答:解:设售价为x元,根据题意列方程得(x-10)(100-
×20)=320,
解得x1=14,x2=18.
故将每件售价定为14或18元时,才能使每天利润为320元.
又题意要求采取提高商品售价减少销售量的办法增加利润,
故应将商品的售价定为18元.
| x-12 |
| 2 |
解得x1=14,x2=18.
故将每件售价定为14或18元时,才能使每天利润为320元.
又题意要求采取提高商品售价减少销售量的办法增加利润,
故应将商品的售价定为18元.
点评:本题考查的是一元二次方程的应用.读懂题意,找到等量关系准确的列出方程是解题的关键.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
某服装店新开张,第一天销售服装a件,第二天的销售件数是第一天销售件数的3倍还多10件,则第二天销售了( )
| A、(a+10)件 |
| B、(3a+13)件 |
| C、(10a+3)件 |
| D、(3a+10)件 |
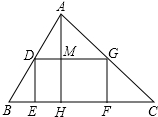 如图一块三角形土地的底边BC=100m,高线AH=80m,现要沿着底边BC修建一座底面是矩形DEFG的大楼,设矩形DEFG的一边长DE=x(m).
如图一块三角形土地的底边BC=100m,高线AH=80m,现要沿着底边BC修建一座底面是矩形DEFG的大楼,设矩形DEFG的一边长DE=x(m).