题目内容
14. 如图,△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C作⊙O的切线,交AB的延长线于点P.
如图,△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C作⊙O的切线,交AB的延长线于点P.(1)求证:∠BCP=∠BAN;
(2)若BP=3,MN=2,CB=6,求AM的长.
分析 (1)由直径所对的圆周角为90°得出∠ANC=90°,由相切得出∠ACP=90°,拆分∠ACP并结合三角形一个外角等于两不相邻的内角和得出结论;
(2)设AB=a,作△BPC底边PC上的高BD,用三角函数表示出BD的长,可用a表示出∠BPC的正弦值,在Rt△ACP中用a表示出∠APC的正弦,即可得出关于a的一元二次方程,解方程可得出AB的长度,再由△BMC∽△CNA可得出BM的长,最后由线段间的关系AB=AM+BM得出结论.
解答 (1)证明:∵AB=AC,
∴∠ABC=∠ACB.
∵PC与⊙O相切于点C,
∴∠ACP=90°,∠BCP=∠ACP-∠ACB=90°-∠ACB.
∵AC为⊙O的直径,
∴∠ANC=90°.
∵∠ANC=∠ABC+∠BAN(外角等于不相邻的两个内角和),
∴∠BAN=∠ANC-∠ABC=90°-∠ABC,
∴∠BCP=∠BAN.
(2)解:过B作BD⊥PC于点D,连接CM,如题所示.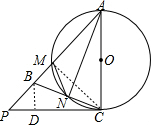
设AB=a,则AC=a,AP=AB+BP=a+3.
∵BD=BP•sin∠BPC=BC•sin∠BCP,
∴$\frac{BP}{BC}$=$\frac{sin∠BCP}{sin∠BPC}$.
在Rt△ANC中,sin∠BAN=$\frac{BN}{AB}$,
∵AB=AC,且AN⊥BC,
∴BN=CN=$\frac{1}{2}$BC=3,
∴sin∠BAN=$\frac{3}{a}$.
∵∠BCP=∠BAN,
∴sin∠BCP=$\frac{3}{a}$.
∵$\frac{BP}{BC}$=$\frac{sin∠BCP}{sin∠BPC}$,
∴sin∠BPC=$\frac{6}{a}$.
∵∠ACP=90°,
∴sin∠APC=$\frac{AC}{AP}$=$\frac{a}{a+3}$=sin∠BPC=$\frac{6}{a}$,
即有a2-6a-18=0,解得:a=3+3$\sqrt{3}$,或a=3-3$\sqrt{3}$(舍去).
∵AC为⊙O的直径,
∴∠AMC=90°,
∴∠BMC=90°=∠CNA.
又∵∠MBC=∠NCA,
∴△BMC∽△CNA,
∴$\frac{BM}{CN}$=$\frac{BC}{CA}$,
∴BM=$\frac{BC•CN}{CA}$=$\frac{6×3}{3+3\sqrt{3}}$=3$\sqrt{3}$-3,
AM=AB-BM=3+3$\sqrt{3}$-(3$\sqrt{3}$-3)=6.
点评 本题考查了切线的性质、角的计算、三角函数、相似三角形的判定及性质,解题的关键是:(1)找出∠BCP90°-∠ACB,∠BAN=90°-∠ABC;(2)设出AB=a,利用三角函数找出关于a的一元二次方程.本题属于中档题,(1)难度不大;(2)难度不小,由于初中阶段没有学习正弦定理,只能运用证正弦定理的方法找出关于a的一元二次方程,找出a后再由相似三角形找出BM的长,从而得出AM的长.解决该类题型的方法是,找到跟所求线段有关的三角形,由相似或者三角函数值找到比例关系即可.

| A. | 浙江卫视“奔跑吧兄弟”综艺节目的收视率,采用抽查的方式 | |
| B. | 了解某渔场中青鱼的平均重量,采用抽查的方式 | |
| C. | 了解iPhone6s手机的使用寿命,采用普查的方式 | |
| D. | 了解一批汽车的刹车性能,采用普查的方式 |
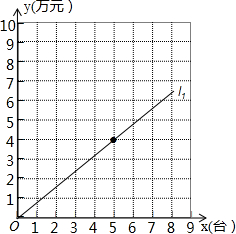 某专营商场销售一种品牌电脑,每台电脑的进货价是0.4万元.图中的直线l1表示该品牌电脑一天的销售收入y1(万元)与销售量x(台)的关系,已知商场每天的房租、水电、工资等固定支出为3万元.
某专营商场销售一种品牌电脑,每台电脑的进货价是0.4万元.图中的直线l1表示该品牌电脑一天的销售收入y1(万元)与销售量x(台)的关系,已知商场每天的房租、水电、工资等固定支出为3万元.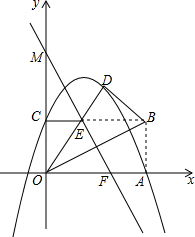 如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),沿着OB翻折△OAB,设翻折后的点A的应对点为点D,OD与BC交于点E,点M在y轴上,直线ME与x轴相交于点F,且∠EMC与∠MOB互余,经过点A,C,D的抛物线的解析式为y=ax2+bx+c.
如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),沿着OB翻折△OAB,设翻折后的点A的应对点为点D,OD与BC交于点E,点M在y轴上,直线ME与x轴相交于点F,且∠EMC与∠MOB互余,经过点A,C,D的抛物线的解析式为y=ax2+bx+c.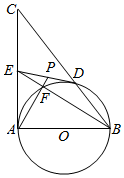 如图,在△ABC中,∠BAC=90°,E是AC的中点,AB是⊙O的直径,⊙O交BC于点D,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.
如图,在△ABC中,∠BAC=90°,E是AC的中点,AB是⊙O的直径,⊙O交BC于点D,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.