Question

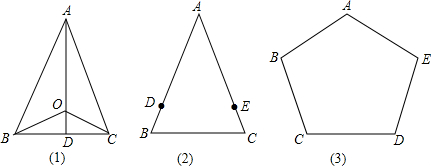
8．（1）如图（1），在△ABC，AB=AC，O为△ABC内一点，且OB=OC，求证：直线AO垂直平分BC．以下是小明的证题思路，请补全框图中的分析过程．

（2）如图（2），在△ABC中，AB=AC，点D、E分别在AB、AC上，且BD=CE．请你只用无刻度的直尺画出BC边的垂直平分线（不写画法，保留画图痕迹）．
（3）如图（3），在五边形ABCDE中，AB=AE，BC=DE，∠B=∠E，请你只用无刻度的直尺画出CD边的垂直平分线，并说明理由．

Answer 1

分析 （1）根据线段垂直平分线的性质定理的逆定理，只要AB=AC，OB=OC即可说明直线AO垂直平分BC；
（2）连结BE、CD相交于点O，则直线AO为BC边的垂直平分线；
（3）连结BD、CE相交于点O，则直线AO为CD边的垂直平分线．先证明ABC≌△AED得到AC=AD，∠ACB=∠ADE，根据等腰三角形的性质得∠ACD=∠ADC，所以∠BCD=∠EDC，再证明△BCD≌△ECD，则∠BDC=∠ECD，所以OD=OC，于是根据线段垂直平分线定理的逆定理即可判断直线AO为CD边的垂直平分线．

解答 解：（1）
（2）如图（2），AO为所作；
（3）如图（3），AO为所作．
在△ABC和△AED中
$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BC=ED}\end{array}\right.$，
∴△ABC≌△AED，
∴AC=AD，∠ACB=∠ADE，
∴∠ACD=∠ADC，
∴∠BCD=∠EDC，
在△BCD和△EDC中，
$\left\{\begin{array}{l}{BC=ED}\\{∠BCD=∠EDC}\\{CD=DC}\end{array}\right.$，
∴△BCD≌△ECD，
∴∠BDC=∠ECD，
∴OD=OC，
∴AO垂直平分CD．

点评 本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此题得关键是运用线段垂直平分线定理的逆定理．