题目内容
3.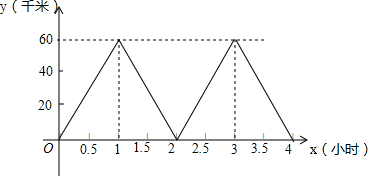 外国语学校1号班车与2号班车每天从初中部出发往返于初中部与高中部两地之间.2号班车比1号班车多往返一趟,如图表示2号班车距初中部的路程y(单位:千米)与所用时间x(单位:小时)之间变化关系的图象.已知1号班车比2号班车晚半小时出发.到达高中部后休息1小时,然后按原路原速返回.结果比2号班车最后一次返回初中部早了半个小时.
外国语学校1号班车与2号班车每天从初中部出发往返于初中部与高中部两地之间.2号班车比1号班车多往返一趟,如图表示2号班车距初中部的路程y(单位:千米)与所用时间x(单位:小时)之间变化关系的图象.已知1号班车比2号班车晚半小时出发.到达高中部后休息1小时,然后按原路原速返回.结果比2号班车最后一次返回初中部早了半个小时.(1)2号班车的速度为60千米/销售;
(2)请在图中画出1号班车距初中部的路程y(千米)与所用时间x(小时)的变化关系的图象;
(3)两车在图中相遇的次数为2次;
(4)求两车最后一次相遇时,距初中部的路程.
分析 (1)由点(1,60)的实际意义可得;
(2)根据1号车晚出发0.5小时、比2号车早到0.5小时可知其函数图象起点为(0.5,0)、终点为(3.5,0),再根据到达高中部后休息1小时且出发和返回速度相同即可画出图形;
(3)根据图象的交点即可判断出相遇的次数;
(4)求出1号车返回时y与x的函数解析式、2号车第二次出发后y与x的函数解析式,再联立方程方程组求解可得.
解答 解:(1)2号班车的速度为$\frac{60}{1}$=60(千米/小时),
故答案为:60;
(2)如图,
(3)由图可知,1号班车与2号班车距初中部的路程y与所用时间x的函数图象有两个交点,
∴两车在途中相遇2次,
故答案为:2;
(4)设1号车返回时y与x的函数解析式为:y=kx+b,
将(2.5,60)、(3.5,0)代入,得:$\left\{\begin{array}{l}{2.5k+b=60}\\{3.5k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-60}\\{b=210}\end{array}\right.$,
∴y=-60x+210,
设2号车第二次出发后y与x的函数解析式为:y=mx+n,
将(2,0)、(3,60)代入,得:$\left\{\begin{array}{l}{2m+n=0}\\{3m+n=60}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=60}\\{n=-120}\end{array}\right.$,
∴y=60x-120,
根据题意,有$\left\{\begin{array}{l}{y=-60x+210}\\{y=60x-120}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{11}{4}}\\{y=45}\end{array}\right.$,
答:两车最后一次相遇时,距初中部的路程为45千米.
点评 本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,相遇问题,读懂题目信息,理解两车的运动过程是解题的关键.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案| A. | 2 | B. | -2 | C. | 2或-2 | D. | 3 |
| A. | 0.5379亿元 | B. | 5.379亿元 | C. | 53.79亿元 | D. | 537.9亿元 |
| A. | 一个平角就是一条直线 | |
| B. | 连接两点间的线段,叫做这两点的距离 | |
| C. | 两条射线组成的图形叫做角 | |
| D. | 经过两点有一条直线,并且只有一条直线 |
| 数量(千克) | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
| 售价(元) | 1.5 | 3 | 4.5 | 6 | 7.5 | 9 | 10.5 | … |
 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是8.
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是8. 有5个边长为1的正方形,排列形式如图:请把它们分割后拼接成一个大正方形.
有5个边长为1的正方形,排列形式如图:请把它们分割后拼接成一个大正方形. 在平面直角坐标系中,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点F,点C与点E分别是对应点(如图所示),观察对应点与点的坐标之间的关系,解答下列问题:
在平面直角坐标系中,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点F,点C与点E分别是对应点(如图所示),观察对应点与点的坐标之间的关系,解答下列问题: 如图,圆锥的底面半径是2cm,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.在这个变化过程中,自变量是圆锥的高,因变量是圆锥的体积.
如图,圆锥的底面半径是2cm,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.在这个变化过程中,自变量是圆锥的高,因变量是圆锥的体积.