题目内容
19.已知方程x2-2x-1=0的两根是x1,x2,不解方程,求下列各式的值:(1)$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$;
(2)(x1-2)(x2-2).
分析 (1)通分后将${{x}_{1}}^{2}+{{x}_{2}}^{2}$变形为(x1+x2)2-2x1x2,再代入即可;
(2)按多项式乘法法则进行计算,并代入即可.
解答 解:∵方程x2-2x-1=0的两根是x1,x2,
∴x1+x2=2,x1•x2=-1,
(1)$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$;
=$\frac{{{x}_{2}}^{2}{{+x}_{1}}^{2}}{{x}_{1}{x}_{2}}$,
=-$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{1}$,
=-(-2)2+2×1,
=-4+2,
=-2;
(2)(x1-2)(x2-2).
=x1x2-2x1-2x2+4,
=-1-2(x1+x2)+4,
=-1-2×2+4,
=-1.
点评 本题考查了根与系数的关系,根据根与系数的关系,找出x1+x2=2、x1•x2=-1是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
8. 若有理数a,b,c在数轴上的对应点A,B,C位置如图,化简|c|-|c-b|+|a+b|=( )
若有理数a,b,c在数轴上的对应点A,B,C位置如图,化简|c|-|c-b|+|a+b|=( )
 若有理数a,b,c在数轴上的对应点A,B,C位置如图,化简|c|-|c-b|+|a+b|=( )
若有理数a,b,c在数轴上的对应点A,B,C位置如图,化简|c|-|c-b|+|a+b|=( )| A. | a | B. | 2b+a | C. | 2c+a | D. | -a |
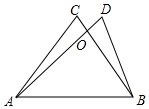 如图,△AOC≌△BOD,∠C与∠D是对应角,AC与BD是对应边,AC=8cm,AD=10cm,OD=OC=2cm,求OB的长.
如图,△AOC≌△BOD,∠C与∠D是对应角,AC与BD是对应边,AC=8cm,AD=10cm,OD=OC=2cm,求OB的长.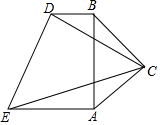 如图,在梯形AEDB中,BD∥AE,∠ABD=90°,在AB的右侧作Rt△ACB,∠ACB=90°,AC=BC,且∠ECD=45°
如图,在梯形AEDB中,BD∥AE,∠ABD=90°,在AB的右侧作Rt△ACB,∠ACB=90°,AC=BC,且∠ECD=45°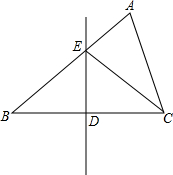 如图,在△ABC中,∠A=60°,边BC的垂直平分线分别交AB,BC于点E,D,连接EC.若∠B=∠ACE,求∠B的度数.
如图,在△ABC中,∠A=60°,边BC的垂直平分线分别交AB,BC于点E,D,连接EC.若∠B=∠ACE,求∠B的度数.