题目内容
如图①所示,已知A、B为直线a上两点,点C为直线a上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1┴a于点D1 ,过点E作EE1┴a于点E1。
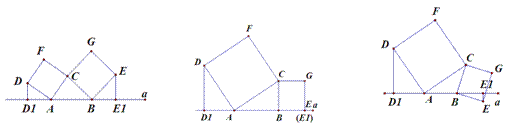 |
图① 图② 图③
⑴如图②,当点E恰好在直线a上时,(此时E1和E重合)。试说明DD1=AB;
⑵如图①中,当D、E两点都在直线a的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由。
⑶如图③,当点E在直线a的 下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系。(不需要证明)
下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系。(不需要证明)
(1)证明:∵四边形CADF、CBEG是正方形,
∴AD=CA,∠DAC=∠ABC=90°, (1分)
∴∠DAD1+∠CAB=90°,
∵DD1⊥AB,
∴∠DD1A=∠ABC=90°, 
∴∠DAD1+∠ADD1=90°,
∴∠ADD1=∠CAB,
在△ADD1和△CAB中,
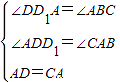 ,
,
∴△ADD1≌△CAB(AAS), (3分)
∴DD1=AB; (4分)
(2)AB=DD1+EE1. (5分)
证明:过点C作CH⊥AB于H,
∵DD1⊥AB,
∴∠DD1A=∠CHA=90°,
∴∠DAD1+∠ADD1=90°,
∵四边形CADF是正方形,
∴AD=CA,∠DAC=90°,
∴∠DAD1+∠CAH=90°,
∴∠ADD1=∠CAH,
在△ADD1和△CAH中,
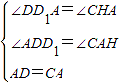 ,
,
∴△ADD1≌△CAH(AAS), (7分)
∴DD1=AH;
同理:EE1=BH, (8分)
∴AB=AH+BH=DD1+EE1; (9分)
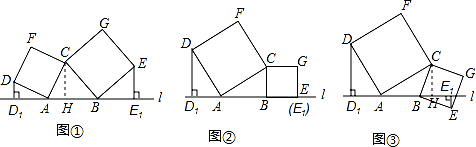
(3)AB=DD1-EE1.(10分)

 (B)
(B) (C)
(C)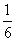 (D)
(D)

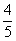 ,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.
,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.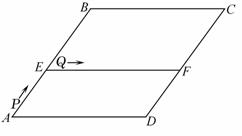 ②以P为圆心,PQ长为半径的⊙P是否能与直线AD相切?如果能,求此时t的值;如果不能,说明理由.
②以P为圆心,PQ长为半径的⊙P是否能与直线AD相切?如果能,求此时t的值;如果不能,说明理由.

 B.
B. C.3
C.3 -
- ×
× =7
=7 与反比例函数
与反比例函数 相交于点A,AB⊥x轴,S△ABC=1,则k的值为 ( )
相交于点A,AB⊥x轴,S△ABC=1,则k的值为 ( ) A.
A. B.
B. C.
C. D.
D.
 ,求⊙P在整个滚动过程中所覆盖部分图形的面积.
,求⊙P在整个滚动过程中所覆盖部分图形的面积.


