题目内容
如图四边形ABCD中，已知∠A=∠C=30°，∠D=60°，AD=8，CD=10．
（1）求AB、BC的长；
（2）已知，半径为1的⊙P在四边形ABCD的外面沿各边滚动（无滑动）一周
，求⊙P在整个滚动过程中所覆盖部分图形的面积．
 | |||
 | |||
解：（1）AB=
，BC=
（2）在⊙P的整个滚动过程中，圆心P的运动路径长为18+
；
所以⊙P在整个滚动过程中，所覆盖部分图形的面积为36+
；
练习册系列答案
巧学巧练系列答案
课课练江苏系列答案
相关题目
如图①所示，已知A、B为直线a上两点，点C为直线a上方一动点，连接AC、BC，分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG，过点D作DD1┴a于点D1 ，过点E作EE1┴a于点E1。
 |
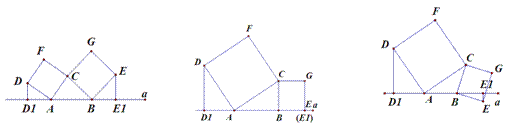图① 图② 图③
⑴如图②，当点E恰好在直线a上时，（此时E1和E重合）。试说明DD1=AB；
⑵如图①中，当D、E两点都在直线a的上方时，试探求三条线段DD1、EE1、AB之间的数量关系，并说明理由。
⑶如图③，当点E在直线a的
下方时，请直接写出三条线段DD1、EE1、AB之间的数量关系。（不需要证明）
B、
C、
D、
根据下列表格中的对应值，判断方程ax2+bx+c=0（a≠0，a，b，c为常数）的根的个数是（ ）
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | 0.02 | 0.01 | 0.02 | 0.04 |
A．0 B．1 C．2 D．1或2
测得∠AEP＝74°，∠BEQ＝30°；在点F处测得∠AFP＝60°，
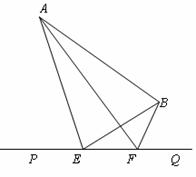
D∥BC（已证）