题目内容

解:(1)∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线.∴DE∥BC. (1’)
又∵E F∥AB,∴四边形DBFE是平行四边形. (3’)
F∥AB,∴四边形DBFE是平行四边形. (3’)
(2)当AB=BC时,四边形DBEF是菱形. (4’)
∵D是AB的中点,∴BD= AB. (5’)
AB. (5’)
∵DE是△ABC的中位线,∴DE= BC. (6’)
BC. (6’)
∵AB=BC,∴BD=DE. (7’)
又∵四边形DBFE是平行四边形,∴四边形DBFE是菱形.(8’)

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
如图①所示,已知A、B为直线a上两点,点C为直线a上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1┴a于点D1 ,过点E作EE1┴a于点E1。
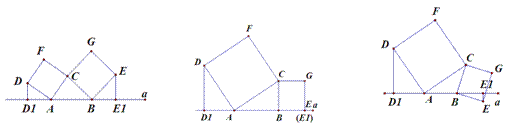 |
图① 图② 图③
⑴如图②,当点E恰好在直线a上时,(此时E1和E重合)。试说明DD1=AB;
⑵如图①中,当D、E两点都在直线a的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由。
⑶如图③,当点E在直线a的 下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系。(不需要证明)
下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系。(不需要证明)
 与x轴、y轴分别交于点A、B,与双曲线
与x轴、y轴分别交于点A、B,与双曲线 (x<0)分别交于点C、D,且C点的坐标为(
(x<0)分别交于点C、D,且C点的坐标为( ,2).
,2). .
.
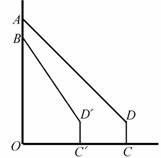
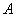 处,此时测得仰角为45°,继续向前走了10m到达
处,此时测得仰角为45°,继续向前走了10m到达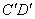 处,发现小明在六楼B处,此时测得仰角为
处,发现小明在六楼B处,此时测得仰角为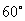 ,已知楼层高AB=2.7m,求O
,已知楼层高AB=2.7m,求O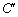 的长.(参考数据:
的长.(参考数据: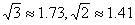 )
) 
 有意义的
有意义的 的取值范围是
的取值范围是 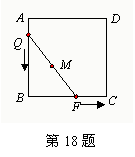
 B.
B. C.
C. D.
D.
 ∠2是对顶角的图形是( )
∠2是对顶角的图形是( )