题目内容
如图,在菱形ABCD中,AB=10,sinA=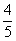 ,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.
,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.
(1)请写出菱形ABCD的面积: ;
(2)若点P从点A出发以1个单位长度/秒的速度沿着线段AB向终点B运动,同时点Q从点E出发也以1个单位长度/秒的速度沿着线段EF向终点F运动,设运动时间为t(秒).
①当t=5时,求PQ的长;
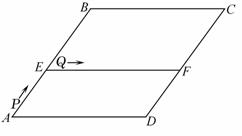 ②以P为圆心,PQ长为半径的⊙P是否能与直线AD相切?如果能,求此时t的值;如果不能,说明理由.
②以P为圆心,PQ长为半径的⊙P是否能与直线AD相切?如果能,求此时t的值;如果不能,说明理由.
(1)80………………………………2分
(2)①根据题意画出图形,如图所示:
 过点P作PM⊥EF,垂足为M
过点P作PM⊥EF,垂足为M
由题意可知AE=4,AP=EQ=5,则EP=1…………3分
∵EF∥AD,
∴∠BEF=∠A,即sin∠BEF=sinA=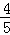 ,
,
即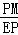 =
=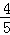 ,则PM=
,则PM=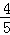 ,……………4分
,……………4分
根据勾股定理得:EM=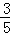 ,……………5分
,……………5分
则MQ=5﹣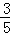 =
=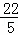 ,
,
在直角三角形PQM中,根据勾股定理得:
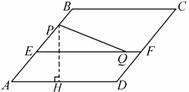 PQ=
PQ=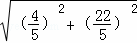 =2
=2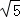 ……………6分
……………6分
②过P作PH⊥AD于H,交EF于G点,
则PH=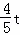 ,PE=t﹣4,PG=
,PE=t﹣4,PG=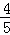 (t﹣4),EG=
(t﹣4),EG=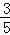 (t﹣4),
(t﹣4),
∴GQ=t﹣EG=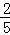 t+
t+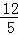 ,
,
PQ2=PG2+GQ2=(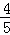 t﹣
t﹣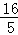 )2+(
)2+(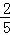 t+
t+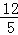 )2,
)2,
由题意可得方程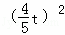 =(
=(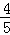 t﹣
t﹣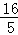 )2+(
)2+(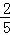 t+
t+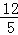 )2,解得:t=10.
)2,解得:t=10.

如图①所示,已知A、B为直线a上两点,点C为直线a上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1┴a于点D1 ,过点E作EE1┴a于点E1。
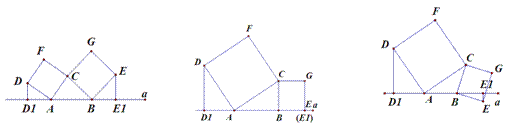 |
图① 图② 图③
⑴如图②,当点E恰好在直线a上时,(此时E1和E重合)。试说明DD1=AB;
⑵如图①中,当D、E两点都在直线a的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由。
⑶如图③,当点E在直线a的 下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系。(不需要证明)
下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系。(不需要证明)
根据下列表格中的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的个数是( )
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | 0.02 | 0.01 | 0.02 | 0.04 |
A.0 B.1 C.2 D.1或2

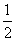 .
.
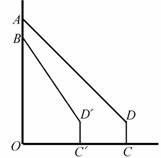
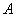 处,此时测得仰角为45°,继续向前走了10m到达
处,此时测得仰角为45°,继续向前走了10m到达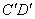 处,发现小明在六楼B处,此时测得仰角为
处,发现小明在六楼B处,此时测得仰角为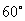 ,已知楼层高AB=2.7m,求O
,已知楼层高AB=2.7m,求O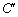 的长.(参考数据:
的长.(参考数据: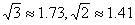 )
) 
 cm,圆心距AB为3cm.则⊙A与⊙B的位置关系是( )
cm,圆心距AB为3cm.则⊙A与⊙B的位置关系是( ) 有意义的
有意义的 的取值范围是
的取值范围是