题目内容
8.将二次函数y=x2-2x+4化成y=(x-h)2+k的形式,则k=3.分析 利用配方法将一次项和二次项组合,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式,得出k的值即可.
解答 解:y=x2-2x+4=(x2-2x+1)-1+4=(x-1) 2+3.
则k=3,
故答案是:3.
点评 本题考查了二次函数的解析式有三种形式:
(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);
(2)顶点式:y=a(x-h)2+k;
(3)交点式(与x轴):y=a(x-x1)(x-x2).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3. 如图,能用ASA来判断△ACD≌△ABE需要添加的条件是( )
如图,能用ASA来判断△ACD≌△ABE需要添加的条件是( )
 如图,能用ASA来判断△ACD≌△ABE需要添加的条件是( )
如图,能用ASA来判断△ACD≌△ABE需要添加的条件是( )| A. | ∠AEB=∠ADC,∠C=∠B | B. | ∠AEB=∠ADC,CD=BE | C. | AC=AB,AD=AE | D. | AC=AB,∠C=∠B |
20.观察字母A、E、H、O、T、W、X、Z,其中不是轴对称的字母有( )个.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
18.用代数式表示“a的平方的2倍与b的差的一半”为( )
| A. | $\frac{1}{2}$(2a-b0 | B. | $\frac{1}{2}$(2a2-b) | C. | 2a2-$\frac{1}{2}$b | D. | (2a)2-$\frac{1}{2}$b |
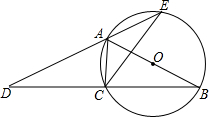 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC,延长DA与⊙O的另一个交点为E,连接AC,CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC,延长DA与⊙O的另一个交点为E,连接AC,CE.