题目内容
2.如图,在平面直角坐标系中,直线AB:y=-x+4与x轴、y轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点且交x轴于另一点C.(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一动点,设点P的横坐标为t,过点P作y轴的平行线交AB于Q,线段PQ的长度为d(d≠0),求d与t之间的函数关系式(不要求写出自变量的取值范围);
(3)在(2)问的条件下,D(m,$\frac{3}{4}m$)为平面直角坐标系内一点,当d取最大值时,直线DP交直线AB于点E,且PD=3DE,求此时D点坐标.
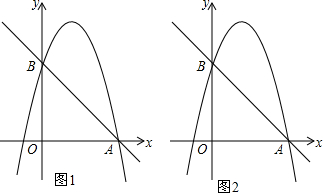
分析 (1)利用一次函数图象上点的坐标特征得到A(4,0),B(0,4),再把A(4,0),B(0,4)代入y=-x2+bx+c得到关于b、c的方程组,解方程组得到b=3,c=4,于是得到抛物线解析式为y=-x2+3x+4;
(2)如图1,根据二次函数图象上点的坐标特征、一次函数图象上点的坐标特征,设P(t,-t2+3t+4),则Q(t,-t+4),则d=-t2+4t;
(3)利用二次函数的性质,由于d=-(t-2)2+4,则当t=2时,d有最大值,此时P点坐标为(2,6),如图2,作DH⊥PQ于H,EF⊥PQ于H,设E(n,-n+4),证明△PDH∽△PEF,利用相似比得到PH=$\frac{3}{4}$PF,DH=$\frac{3}{4}$EF,即6-$\frac{3}{4}$m=$\frac{3}{4}$(6-n+4),m-2=$\frac{3}{4}$(n-2),然后消去n可求出m=$\frac{8}{3}$,于是得到D点坐标为($\frac{8}{3}$,2).
解答 解:(1)当x=0时,y=-x+4=4,则A(4,0);当y=0时,-x+4=0,解得x=4,则B(0,4),
把A(4,0),B(0,4)代入y=-x2+bx+c得$\left\{\begin{array}{l}{-16+4b+c=0}\\{c=4}\end{array}\right.$,解得b=3,c=4,
所以抛物线解析式为y=-x2+3x+4;
(2)如图1,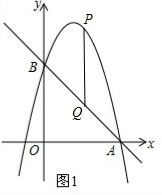
设P(t,-t2+3t+4),则Q(t,-t+4),
所以d=-t2+3t+4-(-t+4)=-t2+4t;
(3)d=-(t-2)2+4,当t=2时,d有最大值,此时P点坐标为(2,6),如图2,作DH⊥PQ于H,EF⊥PQ于H,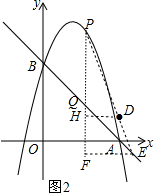
设E(n,-n+4),
∵DH∥EF,
∴△PDH∽△PEF,
∴$\frac{PH}{PF}$=$\frac{DH}{EF}$=$\frac{DP}{PE}$=$\frac{3}{4}$,
即PH=$\frac{3}{4}$PF,DH=$\frac{3}{4}$EF,
∴6-$\frac{3}{4}$m=$\frac{3}{4}$(6-n+4),m-2=$\frac{3}{4}$(n-2),
∴m=$\frac{8}{3}$,
∴D点坐标为($\frac{8}{3}$,2).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、一次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求二次函数解析式,会利用相似比表示线段之间的关系;理解坐标与图形性质.

 阅读快车系列答案
阅读快车系列答案
 如图,点O是直线AB上一点,图中共有5个小于平角的角.
如图,点O是直线AB上一点,图中共有5个小于平角的角. 身高为1.8m 的运动员小王进行投篮训练,已知篮圈中心与地面的垂直距离为3.05 m,小王站在与篮圈中心的水平距离4m的地方进行跳投,球的运动路线一条抛物线,当球运行的水平距离为2.5m时,球达到距离地面3.5m的最高点,运行一段时间后篮球最后恰好落入篮圈.
身高为1.8m 的运动员小王进行投篮训练,已知篮圈中心与地面的垂直距离为3.05 m,小王站在与篮圈中心的水平距离4m的地方进行跳投,球的运动路线一条抛物线,当球运行的水平距离为2.5m时,球达到距离地面3.5m的最高点,运行一段时间后篮球最后恰好落入篮圈. 如图,△ABC的角平分线交于点P,已知AB,BC,CA的长分别为5,7,6,则S△ABP:S△ACP:S△BCP=5:6:7.
如图,△ABC的角平分线交于点P,已知AB,BC,CA的长分别为5,7,6,则S△ABP:S△ACP:S△BCP=5:6:7.