题目内容
11．
如图，△ABC的角平分线交于点P，已知AB，BC，CA的长分别为5，7，6，则S△ABP：S△ACP：S△BCP=5：6：7．
分析 过P作PF⊥AC于F，PE⊥BC于E，PD⊥AB于D，根据角平分线性质求出PD=PE=PF，根据三角形面积公式求出S△ABP：S△ACP：S△BCP=AB：AC：BC，代入求出即可．
解答 解：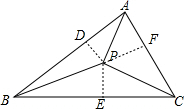
过P作PF⊥AC于F，PE⊥BC于E，PD⊥AB于D，
∵△ABC的角平分线交于点P，
∴PD=PE=PF，
∵S△ABP=$\frac{1}{2}$×AB×PD，S△ACP=$\frac{1}{2}$×AC×PF，S△BCP=$\frac{1}{2}$×BC×PE，
∴S△ABP：S△ACP：S△BCP=AB：AC：BC=5：6：7，
故答案为：5：6：7．
点评 本题考查了角平分线的性质的应用，熟练掌握三角形角平分线的性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，∠MON=30°，点B1、B2、B3…和A1、A2、A3…分别在OM和ON上，且△A1B1A2、△A2B2A3、△A3B3A4、…分别为等边三角形，已知OA1=1，则△A2014B2014A2015的边长为22013．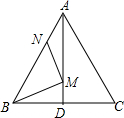
如图，在等边△ABC中，AB=4，N为线段AB上的任意一点，∠BAC的平分线交BC于点D，M是AD上的动点，连结BM、MN，则BM+MN的最小值是2$\sqrt{3}$．
如图，在等腰△ABC中，AB=AC，∠A=40°，BD⊥AC于点D，则∠CBD=20°．