题目内容
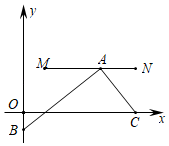
【题目】如图,在平面直角坐标系中,M、N、C三点的坐标分别为(![]() ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A.![]() ≤b≤1B.
≤b≤1B.![]() ≤b≤1C.
≤b≤1C.![]() ≤b≤
≤b≤![]() D.
D.![]() ≤b≤1
≤b≤1
【答案】B
【解析】
延长NM交y轴于P点,则MN⊥y轴.连接CN.证明△PAB∽△NCA,得出![]() ,设PA=x,则NA=PN﹣PA=3﹣x,设PB=y,代入整理得到y=3x﹣x2=﹣(x﹣
,设PA=x,则NA=PN﹣PA=3﹣x,设PB=y,代入整理得到y=3x﹣x2=﹣(x﹣![]() )2+
)2+![]() ,根据二次函数的性质以及
,根据二次函数的性质以及![]() ≤x≤3,求出y的最大与最小值,进而求出b的取值范围.
≤x≤3,求出y的最大与最小值,进而求出b的取值范围.
解:如图,延长NM交y轴于P点,则MN⊥y轴.连接CN.
在△PAB与△NCA中,
![]() ,
,
∴△PAB∽△NCA,
∴![]() ,
,
设PA=x,则NA=PN﹣PA=3﹣x,设PB=y,
∴![]() ,
,
∴y=3x﹣x2=﹣(x﹣![]() )2+
)2+![]() ,
,
∵﹣1<0,![]() ≤x≤3,
≤x≤3,
∴x=![]() 时,y有最大值
时,y有最大值![]() ,此时b=1﹣
,此时b=1﹣![]() =﹣
=﹣![]() ,
,
x=3时,y有最小值0,此时b=1,
∴b的取值范围是﹣![]() ≤b≤1.
≤b≤1.
故选:B.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目