题目内容
如果式子
+|x-2|化简的结果为3-2x，则x的取值范围是 ．
| (x-1)2 |
考点：二次根式的性质与化简
专题：
分析：利用绝对值的性质结合二次根式的性质化简求出即可．
解答：解：∵
+|x-2|化简的结果为3-2x，
∴
+|x-2|=1-x+2-x=3-2x，
∴1-x≥0，2-x≥0，
解得：x≤1．
故答案为：x≤1．
| (x-1)2 |
∴
| (x-1)2 |
∴1-x≥0，2-x≥0，
解得：x≤1．
故答案为：x≤1．
点评：此题主要考查了二次根式的性质与化简，正确掌握二次根式性质是解题关键．
练习册系列答案
导学教程高中新课标系列答案
相关题目
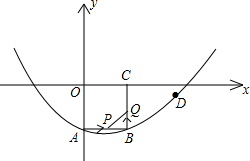如图，在平面直角坐标系xOy中，正方形OABC的边长为2cm，点A、C分别在y轴的负半轴和x轴的正半轴上，抛物线y=ax2+bx+c经过点A、B和D（4，-下列各式从左到右的变形中，属于因式分解的是（ ）
| A、（x-1）（x+1）=x2-1 |
| B、（a+b）2=a2+2ab+b2 |
| C、x2-x-2=（x+1）（x-2） |
| D、ax-ay-1=a（x-y）-1 |
