题目内容
 两块完全相同的等腰三角形放成如图样子,假设图形中的所有点、线、面都在同一平面内,指出图中相似不正确的是( )
两块完全相同的等腰三角形放成如图样子,假设图形中的所有点、线、面都在同一平面内,指出图中相似不正确的是( )| A、△DAE∽△DCA |
| B、△EAD∽△EBA |
| C、△BAD∽△CAE |
| D、△BAE∽△CDA |
考点:相似三角形的判定
专题:
分析:根据等腰直角三角形的性质得到∠B=∠C=∠F=∠FAG=45°,∠BAC=∠AGF=90°,则可根据有两组角对应相等的两个三角形相似,判断△DAE∽△DCA,△EAD∽△EBA;根据△DAE∽△DCA得到∠DEA=∠DAC,加上∠B=∠C,则可得到△BAE∽△CDA;不能判断△BAD∽△CAE.
解答:解:∵△ABC和△FAG是全等的等腰直角三角形,
∴∠B=∠C=∠F=∠FAG=45°,∠BAC=∠AGF=90°,
∵∠DAE=∠DCA,
而∠ADE=∠CDA,
∴△DAE∽△DCA,
同理可得△EAD∽△EBA;
∵∠BAD+∠CAE=45°,
∴不能判断△BAD∽△CAE;
∵△DAE∽△DCA,
∴∠DEA=∠DAC,
而∠B=∠C,
∴△BAE∽△CDA.
故选C.
∴∠B=∠C=∠F=∠FAG=45°,∠BAC=∠AGF=90°,
∵∠DAE=∠DCA,
而∠ADE=∠CDA,
∴△DAE∽△DCA,
同理可得△EAD∽△EBA;
∵∠BAD+∠CAE=45°,
∴不能判断△BAD∽△CAE;
∵△DAE∽△DCA,
∴∠DEA=∠DAC,
而∠B=∠C,
∴△BAE∽△CDA.
故选C.
点评:本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了等腰直角三角形的性质.

练习册系列答案
相关题目
下列各式符合代数式书写规范的是( )
A、
| ||
| B、a×3 | ||
| C、2m-1个 | ||
D、1
|
下列各式由左边到右边的变形中,是因式分解的为( )
| A、(2a+3)(2a-3)=4a2-9 |
| B、-3a2b3c=(-3abc)(ab2) |
| C、a2-2a+1=a(a-2)+1 |
| D、6a2b-3ab2=3ab(2a-b) |
 如图抛物线y=-x2+bx+c的图象与x轴的一个交点(1,0),则抛物线与x轴的另一个交点坐标是
如图抛物线y=-x2+bx+c的图象与x轴的一个交点(1,0),则抛物线与x轴的另一个交点坐标是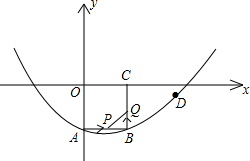 如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,-
如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,-