题目内容
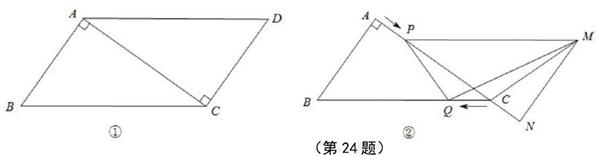
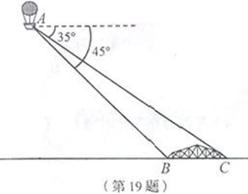
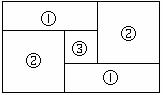
已知:如图①,在□ABCD中,AB=3cm,BC=5cm.AC⊥AB。△ACD沿AC的方向匀速平移得到
△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速运动,速度为1cm/s,当△PNM停止平移时,点Q也停止运动.如图②,设运动时间为t(s)(0<t<4).解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S△QMC∶S四边形ABQP=1∶4?若存在,求出t的值;
若不存在,请说明理由.
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
解:(1)在Rt△ABC中,由勾股定理得: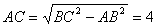
由平移性质可得MN∥AB
因为PQ∥MN,所以PQ∥AB,所以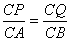 ,即
,即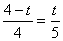 ,解得
,解得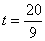
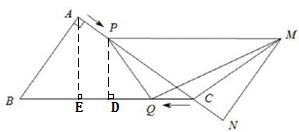 (2)作PD⊥BC于点D,AE⊥BC于点E
(2)作PD⊥BC于点D,AE⊥BC于点E
由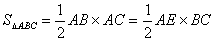 可得
可得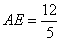
则由勾股定理易求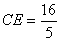
因为PD⊥BC,AE⊥BC
所以AE∥PD,所以△CPD∽△CAE
所以 ,即
,即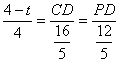
求得: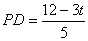 ,
,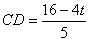
因为PM∥BC,所以M到BC的距离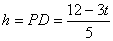
所以,△QCM是面积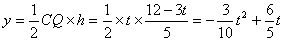
(3)因为PM∥BC,所以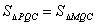
若S△QMC∶S四边形ABQP=1∶4,则S△QMC∶S△ABC=1∶5
即: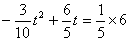 ,整理得:
,整理得: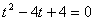 ,解得
,解得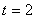
答:当t=2时,S△QMC∶S四边形ABQP=1∶4
(4)若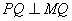 ,则∠MDQ=∠PDQ=90°
,则∠MDQ=∠PDQ=90°
因为MP∥BC,所以∠MPQ=∠PQD,
所以△MQP∽△PDQ,所以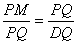 ,所以
,所以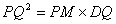
即: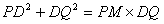 ,由
,由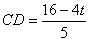 ,所以DQ = CD-CQ
,所以DQ = CD-CQ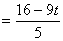
故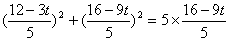 ,整理得
,整理得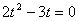
解得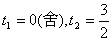
答:当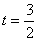 时,
时,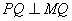 。
。

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 可变形为
可变形为 B.
B.  C.
C.  D.
D. 
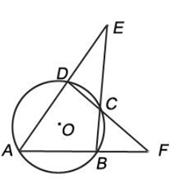
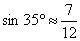 ,
, 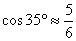 ,
,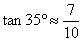
 A.
A.  B.
B.  C.
C.  D.
D. 
 D.
D.