题目内容
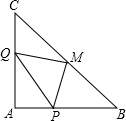 已知在Rt△ABC中,∠A=90°,AB=3,AC=4,P、Q分别为边AB、AC上一点,PQ∥BC,M为斜边BC上的一点,若△MPQ为等腰直角三角形,则PQ的长度为
已知在Rt△ABC中,∠A=90°,AB=3,AC=4,P、Q分别为边AB、AC上一点,PQ∥BC,M为斜边BC上的一点,若△MPQ为等腰直角三角形,则PQ的长度为考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:作ME⊥AC,MF⊥AB,易证△QME≌△PMF,即可求得AE的长,再根据PQ∥BC,可以求得AQ和AP的长,根据勾股定理即可求得PQ的长.
解答:解:作ME⊥AC,MF⊥AB,
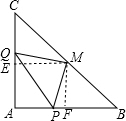
∵∠QME+∠EMP=90°,∠EMP+∠PMF=90°,
∴∠QME=∠PMF,
在△QME和△PMF中,
,
∴△QME≌△PMF(AAS),
∴EM=FM,即AE=AF,
设AE=x,则
=
,即
=
,
解得:x=
,
∵PQ∥BC,∴
=
,整理得:
=
,
∴
=
,
解得:EQ=
,
∴AQ=AE+EQ=
,AP=AF-PF=
,
∴PQ=
=
.
故答案为
.

∵∠QME+∠EMP=90°,∠EMP+∠PMF=90°,
∴∠QME=∠PMF,
在△QME和△PMF中,
|
∴△QME≌△PMF(AAS),
∴EM=FM,即AE=AF,
设AE=x,则
| CE |
| AC |
| EM |
| AB |
| 3-x |
| 3 |
| x |
| 4 |
解得:x=
| 12 |
| 7 |
∵PQ∥BC,∴
| AQ |
| AC |
| AP |
| AB |
| AQ |
| AP |
| 4 |
| 3 |
∴
| AE+EQ |
| AF-AP |
| 4 |
| 3 |
解得:EQ=
| 12 |
| 49 |
∴AQ=AE+EQ=
| 96 |
| 49 |
| 72 |
| 49 |
∴PQ=
| AQ2+AP2 |
| 120 |
| 49 |
故答案为
| 120 |
| 49 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了勾股定理的运用,本题中求证△QME≌△PMF是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,图中共有三角形( )
如图,图中共有三角形( )| A、4个 | B、5个 | C、6个 | D、8个 |
反比例函数y=-
的图象过点(2,-m),则m的值是( )
| 4 |
| x |
| A、1 | B、2 | C、-2 | D、4 |
 如图,矩形草坪的长是80m,宽是10m,现要修建一条平行于草坪边缘的矩形小路,使得小路矩形与草坪矩形相似,求小路的宽.
如图,矩形草坪的长是80m,宽是10m,现要修建一条平行于草坪边缘的矩形小路,使得小路矩形与草坪矩形相似,求小路的宽. 如图,已知△ABC中,M为BC的中点,AD是角平分线,MF⊥AD交AD的延长线于点F,交AB于点E,求证:BE=
如图,已知△ABC中,M为BC的中点,AD是角平分线,MF⊥AD交AD的延长线于点F,交AB于点E,求证:BE=
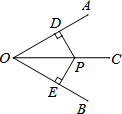 如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若OD=8,OP=10,则PE=
如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若OD=8,OP=10,则PE=