题目内容
16．估计$\sqrt{10}$的值在（ ）| A． | 2到3之间 | B． | 3到4之间 | ||
| C． | 2到3之间或-3到-2之间 | D． | 3到4之间或-4到-3之间 |
分析 依据被开放数越大对应的算术平方根越大求解即可．
解答 解：∵9＜10＜16，
∴3＜$\sqrt{10}$＜4．
故选：B．
点评 本题主要考查的是估算无理数的大小，夹逼法的应用是解题的关键．
练习册系列答案
相关题目
6．
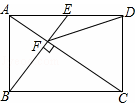如图，点E是矩形ABCD的边AD的中点，且BE⊥AC于点F，则下列结论中错误的是（ ）
如图，点E是矩形ABCD的边AD的中点，且BE⊥AC于点F，则下列结论中错误的是（ ）| A． | AF=$\frac{1}{2}$CF | B． | ∠DCF=∠DFC | ||
| C． | 图中与△AEF相似的三角形共有4个 | D． | tan∠CAD=$\frac{\sqrt{2}}{2}$ |
4．已知圆锥的底面半径为4，母线长为12，则圆锥的侧面展开图的圆心角为（ ）
| A． | 60° | B． | 90° | C． | 120° | D． | 216° |
11．小明想用最大刻度为100℃的温度计测量食用油的沸点温度（远高于100℃），显然不能直接测量，于是他想到了另一种方法．把常温10℃的食用油放在锅内用煤气灶均匀地加热，开始加热后，每隔10s测量一次油温，共测量了4次，测得的数据如下：
他测量出把油烧到沸腾所需要的时间是160s，这样就可以确定该食用油的温度．
（1）写出w与r的函数解析式．
（2）求这种食用油沸点的温度．
| 时间t/s | 0 | 10 | 20 | 30 |
| 油温w/℃ | 10 | 25 | 40 | 55 |
（1）写出w与r的函数解析式．
（2）求这种食用油沸点的温度．
1．若分式$\frac{x+2}{x-1}$有意义，则x的取值范围是（ ）
| A． | x≥1 | B． | x≠1 | C． | x≥-2 | D． | x≠-2 |
8．估计$\sqrt{14}$的值在哪两个数之间（ ）
| A． | 1与2 | B． | 2 与3 | C． | 3与4 | D． | 4与5 |
如图，以等腰三角形ABC的底边BC为直径的圆O分别交两腰于D、E，连结DE，求证：