题目内容
抛物线开口向上,顶点坐标是(1,3),则函数y随自变量x的增大而减小的x的取值范围是( )
| A、x>3 | B、x<3 |
| C、x>1 | D、x<1 |
考点:二次函数的性质
专题:
分析:根据开口向上可知在对称轴左侧y随x的增大而减小,由顶点坐标可求得其对称轴,可得出答案.
解答:解:
∵顶点坐标是(1,3),
∴对称轴方程为x=1,
∵抛物线开口向上,
∴在对称轴左侧y随x的增大而减小,
∴x<1,
故选D.
∵顶点坐标是(1,3),
∴对称轴方程为x=1,
∵抛物线开口向上,
∴在对称轴左侧y随x的增大而减小,
∴x<1,
故选D.
点评:本题主要考查二次函数的增减性,掌握在对称轴两侧的增减性是解题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
到三角形三个顶点距离相等的点是( )
| A、三角形三条边的垂直平分线的交点 |
| B、三角形三条角平分线的交点 |
| C、三角形三条高的交点 |
| D、三角形三条边的中线的交点 |
下列计算正确的是( )
| A、(-5)-5=0 | ||
B、(-
| ||
| C、2-(-1)=-3 | ||
| D、-23=-6 |
式子
×
×5=
×5×
这里应用了( )
| 3 |
| 5 |
| 1 |
| 6 |
| 3 |
| 5 |
| 1 |
| 6 |
| A、乘法分配律 |
| B、乘法交换律 |
| C、乘法结合律 |
| D、乘法的性质 |
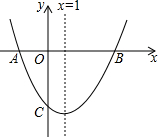 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.