题目内容
19. 如图,CD平分∠ACB,交AB于点D,AE∥DC,AE与BC的延长线相交于点E,∠ACE=80°,求∠CAE的度数.
如图,CD平分∠ACB,交AB于点D,AE∥DC,AE与BC的延长线相交于点E,∠ACE=80°,求∠CAE的度数.
分析 根据邻补角的定义求得∠ACB=100°;然后利用角平分线的定义求得∠DCA=50°;最后由平行线的性质和等量代换求得∠CAE的度数.
解答 解:∵∠ACE=80°(已知),
∴∠ACB=100°(邻补角的定义),
又∵CD平分∠ACB(已知),
∴∠DCA=100°×$\frac{1}{2}$=50°,
∵AE∥DC(已知),
∴∠CAE=∠DCA=50°(两直线平行,内错角相等).
点评 本题主要考查了平行线的性质和角平分线的定义,利用邻补角的定义求得∠ACB=100°是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
10.矩形具有而平行四边形不具有的性质是( )
| A. | 两组对边分别平行 | B. | 两组对角分别相等 | ||
| C. | 对角线互相平分 | D. | 对角线相等 |
11.用一副三角板不能画出( )
| A. | 15°角 | B. | 135°角 | C. | 145°角 | D. | 105°角 |
 如图,在周长为18cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为9cm.
如图,在周长为18cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为9cm.
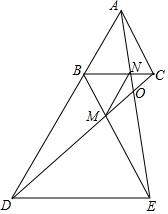 如图,点B在AD上,△ABC和△BDE是等边三角形,CD交BE于点M,AE交BC,CD于点N,O,连接MN.
如图,点B在AD上,△ABC和△BDE是等边三角形,CD交BE于点M,AE交BC,CD于点N,O,连接MN.