题目内容
11．如图，每个图案都由若干个棋子摆成，依照此规律，第n个图案中棋子的总个数y与n的关系式为y=n（n+1）．
分析 从每个图案的横队和纵队棋子个数分析与n的关系．
解答 解：每个图案的纵队棋子个数是：n，
每个图案的横队棋子个数是：n+1，
那么第n个图案中棋子的总个数y与n的关系式为y=n（n+1）．
故答案为：y=n（n+1）．
点评 本题主要考查图形的变化规律：首先应找出图形哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．探寻规律要认真观察、仔细思考，善于联想来解决这类问题．
练习册系列答案
相关题目
1．二次函数y=-（x-3）2+1的最大值为（ ）
| A． | x=3 | B． | x=1 | C． | y=3 | D． | y=1 |
6．已知抛物线y=（m+1）x${\;}^{{m^2}+m}}$有最高点，则m的值是（ ）
| A． | m＜-1 | B． | m=1 | C． | m=-2 | D． | m=1或m=-2 |
3．下列函数中，是二次函数的是（ ）
| A． | y=2x | B． | y=${x^2}+\frac{1}{x}$ | C． | y=$\sqrt{{x}^{2}-2x+1}$ | D． | y=x2-2 |
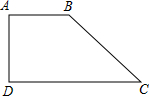如图，在四边形ABCD中，AB∥DC，∠D=90°，BC=$\sqrt{10}$，AB=4，tanC=$\frac{1}{3}$，求四边形ABCD的面积．