题目内容
7.如图1,P为平行四边形ABCD内一点,PB=AB,∠ABP=∠ADP=90°.(1)请在四边形ABPD内画一条线段,把四边形ABPD分成两部分,再将这两部分重新拼成一个正方形,画出简图并说明理由;
(2)如图2,连结PC,求∠BCP的度数.

分析 (1)如图1,过点B作BE⊥AD于E,延长DP交BC于F,线段BE把四边形ABPD分成△ABE和四边形BEDP,将△BAE绕点B顺时针旋转90°到△BPF的位置,由平行四边形的性质得到∠EBC=90°,再理由等角的余角相等得到∠ABE=∠PBF,则可证明△BAE≌△BPF,所以BE=BF,于是可判定四边形BEDF为正方形;
(2)延长DP交BC于F,如图2,同样方法可证明△DCF≌△BPF得到CF=PF,则△PCF为等腰直角三角形,从而得到∠BCP=45°.
解答 解:(1)如图1,过点B作BE⊥AD于E,延长DP交BC于F,线段BE把四边形ABPD分成△ABE和四边形BEDP,将△BAE绕点B顺时针旋转90°到△BPF的位置,则四边形BEDF为正方形.
理由如下:
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴BE⊥BC,
∴∠EBC=90°,
∵∠ADP=90°.
∴∠DFB=90°,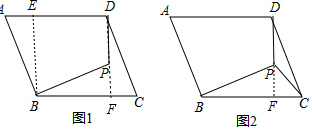 ∵∠ABP=90°.
∵∠ABP=90°.
∴∠ABE=∠PBF,
在△BAE和△BPF中
$\left\{\begin{array}{l}{∠AEB=∠PFB}\\{∠ABE=∠PBF}\\{BA=BP}\end{array}\right.$,
∴△BAE≌△BPF,
∴BE=BF,
∴四边形BEDF为正方形;
(2)延长DP交BC于F,如图2,
与(1)一样可证明△DCF≌△BPF,
∴CF=PF,
∴△PCF为等腰直角三角形,
∴∠BCP=45°.
点评 本题考查了复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了正方形的判定.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | 对角线互相垂直的四边形是平行四边形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线相等且互相垂直的四边形是菱形 | |
| D. | 对角线相等且互相垂直的平行四边形是正方形 |
15.$\frac{\sqrt{2}}{2}$,38,0,π,$\sqrt{16}$,$\frac{1}{3}$,0.1010010001…(相连两个1之间依次多一个0),其中无理数有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.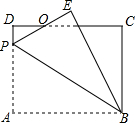 如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
 如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )| A. | 4.8 | B. | 3$\sqrt{2}$ | C. | 5 | D. | 3$\sqrt{3}$ |
