题目内容
8.某市为了鼓励市民节约用水,规定自来水的收费标准如下表:| 每月每户用水量 | 每吨价(元) |
| 不超过10吨部分 | 0.50 |
| 超过10吨而不超过20吨部分 | 0.75 |
| 超过20吨部分 | 1.50 |
(2)写出每月每户的水费y(元)与用水量x(吨)之间的关系式;
(3)若小明家每月缴水费17元,问:他家该月用水多少吨?
分析 (1)根据表格可知他家用水的花费=前10吨的费用+超过10吨的10吨部分的花费+超过20吨的2吨部分的花费;
(2)每月每户的水费分成3部分交费,分别列出函数关系式即可;
(3)首先通过计算讨论出他交水费17元所用的水的吨数所在范围,再利用函数关系式计算即可.
解答 解:(1)0.5×10+0.75×10+1.50×(22-20)=15.5(元);
(2)y=$\left\{\begin{array}{l}{0.5x(0≤x≤10)}\\{0.5×10+0.75(x-10)(10<x≤20)}\\{0.5×10+0.75(20-10)+1.50(x-20)(x>20)}\end{array}\right.$;
(3)0.5×10=5(元),
0.5×10+0.75×(20-10)=12.5(元),
∵17>12.5,
∴他家用水必定超过了20吨,
设他家用水a吨,由题意得:
0.50×10+0.75(20-10)+1.50(a-20)=17,
解得:a=23.
答:他家五月份用水23吨.
故答案为:15.5.
点评 此题主要考查了一次函数的应用,根据实际问题列函数关系式,关键是看懂图表的意思,分情况分别列出函数关系式.

练习册系列答案
相关题目
18.如果用+0.02克表示一只乒乓球质量超出标准质量0.02克,那么一只乒乓球质量低于标准质量0.02克记作( )
| A. | -0.02克 | B. | +0.02克 | C. | 0克 | D. | +0.04克 |
3.一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价),经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:
(1)求y关于x的函数关系式;
(2)写出该公司销售这种产品的年利润W(万元)关于销售单价X(元)的函数关系式;当销售单价X为何值时,年利润最大?
(3)要使年利润不低于60万元,请求出该公司产品的销售单价范围.
| 销售单价x(元) | 50 | 60 | 70 | 80 |
| 年销售量y(万件) | 5.5 | 5 | 4.5 | 4 |
(2)写出该公司销售这种产品的年利润W(万元)关于销售单价X(元)的函数关系式;当销售单价X为何值时,年利润最大?
(3)要使年利润不低于60万元,请求出该公司产品的销售单价范围.
13.化简$\frac{{x}^{2}}{x-1}$-x+1的结果是( )
| A. | $\frac{1}{x-1}$ | B. | $\frac{1}{1-x}$ | C. | $\frac{1-2x}{x-1}$ | D. | $\frac{2x-1}{x-1}$ |
20.估算$\sqrt{30}$的值在( )
| A. | 3和4之间 | B. | 4和5之间 | C. | 5和6之间 | D. | 6和7之间 |
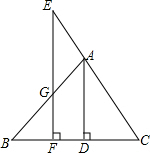 如图,已知AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠E=∠AGE,求证:∠BAD=∠CAD.
如图,已知AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠E=∠AGE,求证:∠BAD=∠CAD.