题目内容
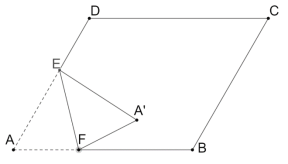
【题目】如图,在![]() 中,
中,![]() ,作
,作![]() 点关于直线
点关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() .过
.过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,若
,若![]()
![]() ,
,![]()
![]() ,则
,则![]() 的周长是_____
的周长是_____ ![]() .
.
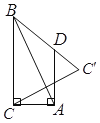
【答案】![]()
【解析】
由勾股定理可求出AB的长,根据轴对称,可得到全等三角形,通过作辅助线构造全等三角形,从而得到AD=BD,设未知数,由勾股定理列方程,求出AD,进而计算三角形的周长.
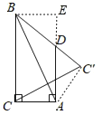
过点B作BE⊥AD,交AD的延长线于点E,连接AC′,则∠E=90![]() ,
,
∵C、C'关于直线AB对称,
∴△ABC≌△ABC′,
∴AC=AC′=4,BC=BC′=8,∠BCA=∠BC′A=90![]() =∠E,
=∠E,
∴四边形ACBE是矩形,
∴BE=AC=4,
∵∠BDE=∠ADC′
∴△BDE≌△ADC′(AAS),
∴BD=AD,
设BD=x,则DE=8x,
在Rt△BDE中,由勾股定理得:x2=(8x)2+42,
解得:x=5,即:AD=BD=5,
在Rt△ABC中,AB=![]() =
=![]() ,
,
△ABD的周长=AB+BD+AD=![]() +5+5=
+5+5=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某礼品店从文化用品市场批发甲、乙、丙三种礼品(每种礼品都有),各礼品的数量和批发单价列表如下:
甲 | 乙 | 丙 | |
数量(个) |
|
|
|
批发单价(元) |
|
|
|
|
![]() 当
当![]() 时,若这三种礼品共批发
时,若这三种礼品共批发![]() 个,甲礼品的总价不低于丙礼品的总价,求
个,甲礼品的总价不低于丙礼品的总价,求![]() 的最小值.
的最小值.
![]() 已知该店用
已知该店用![]() 元批发了这三种礼品,且
元批发了这三种礼品,且![]() .
.
![]() 当
当![]() 时,若批发这三种礼品的平均单价为
时,若批发这三种礼品的平均单价为![]() 元/个,求
元/个,求![]() 的值.
的值.
![]() 当
当![]() 时,若该店批发了
时,若该店批发了![]() 个丙礼品,且
个丙礼品,且![]() 为正整数,求
为正整数,求![]() 的值.
的值.